Blog

The first part of this contribution recalls the definition of endogenous money given by the monetary circuit¹ and retained by Augusto Graziani. It then describes what could be called the “canonical” version of the model of the circuit he developed, which provides a concise description of the functioning of a macroeconomy that fully integrates money and banks. The second part presents some empirical evidence of the monetary circuit. Looking to possible future developments, the third part presents some ideas on the potential use of the monetary circuit theory for the social evaluation of banking operations

1. Theoretical aspects of the monetary circuit

1.1 General observations

Banking operations are a particular type of financial transactions, and as noted by de Finetti:

“Financial operations boil down to exchanges of money; to consider them in their broadest possible sense, we could even define financial operations as those exchange contracts in which no commodity appears except money,” De Finetti (1935, p. 471).²

To assess the social welfare aspects of banking activity, it is therefore necessary to have a model that fully integrates money and banks and explains how they relate to the rest of the economic and social system. Contrary to many mainstream approaches, Graziani’s monetary circuit meets these two requirements³. As recalled by Riccardo Bellofiore (2022), Graziani’s circuit is an economic model with two goods (consumption and investment) and three institutional sectors or poles: households⁴, banks, and firms (non-financial corporations). In this logical framework, money is defined as a liability issued by the banking sector, which is used as a means of payment between households and firms precisely because it is external to their transactions (triangular definition of money). The specific role of banks in this context is to produce the means of payment necessary to realize market transactions by issuing a “liquid” liability created when they grant a credit. The latter is an illiquid asset in the balance sheet of banks, unlike the corresponding monetary liability⁵.

1.1.1  The “systemic” dimension of Graziani’s circuit

Within the economic system, Graziani focuses on the main monetary variables, which he analyses in detail, effectively developing what can be termed in the macroeconomic jargon as the “monetary and financial block” of a larger macroeconomic model⁶. In principle, this allows to integrate the monetary circuit within a variety of models of different types, because the block of equations explaining monetary variables can be inserted into schemes that can vary from short-term neoclassical models to long-term models à la Garegnani or Pasinetti⁷.

But while concentrating on monetary aspects, Graziani’s economic analysis does not lose sight of the systemic dimensions. Post-Keynesians like Eichner (1991) or Mockers (2016), but also much of classical and neoclassical economics, and particularly Leontief models, have embraced the idea of applying systems theory to economics. It is also noteworthy that the French literature, which Graziani knew very well, has long identified the systemic character of the circuit, and particularly Poulon (2015, pp. 9-94), one of the founders of the circuit, goes so far as to oppose the “systemic paradigm” of the circuit to the “set theory” of general equilibrium⁸.

It can be said of Graziani that, while primarily developing the analysis of the monetary and financial sector, he reasons in the macroeconomic logic of a full general economic system. In fact, one of his most Keynesian conclusions, repeated in various writings (notably 2003b), is that, precisely because of the integration of money, a systemic effect is created whereby in a monetary economy the whole is no longer the sum of the parts⁹. Money is thus an element that explains the “fallacy of composition” highlighted by Keynesian analysis¹⁰.

1.1.2 Main features of money in the circuit

It’s useful to recall a few important features of money in Augusto Graziani’s circuit.

1.1.2.1 Sequential time: In the circuit, money is defined in a triangular exchange (see §1.1.2.5). It is created endogenously, circulates, and it is destroyed or accumulated in a sequence of phases (§1.1.2.2) and periods developing in historical time. In this regard, Graziani’s circuit differs from the one of Bernard Schmitt (1984), which unfolds in the so-called quantum time, while it is very close to that of Alain Parguez (1996 and 2000, with Seccareccia) and of Poulon (2015). Because of its sequential character, the model of the circuit admits a causality, which in principle is precluded in simultaneous models. This is relevant for policy purposes, as, strictly speaking, a causality relationship is the necessary logical premise for discussing the effect of an economic policy instrument (ideally an exogenous variable) on a target variable (which would normally be endogenous) ¹¹.

1.1.2.2 Emphasis on the single period: Like the other original founders of the circuit (Schmitt, Parguez and Poulon), Graziani is mainly interested in dynamics, but focuses on a single period, which he chooses to be the initial one “at the origin of times”, analysing it and breaking it down into various phases, which are also sequential. In this time sequence, money is created and circulates as a mean of payment, first as income and then as consumption or saving, being partially or totally destroyed at the end of the period. The sequence reveals the dual nature of the endogenous money of the circuit, both as a flow and as a stock (Graziani, 1996 and 2002). At the end of the single period, if all money initially created is destroyed, a state of equilibrium prevails described in the article published in Italian under the title Money without crisis (Graziani 1984b). Otherwise, the conditions for a “crisis” emerge, described in the introduction to Costabile’s 1980 book on Malthus¹². In both cases, once the initial “single” period is over, other periods follow. Thus, depending on whether the first period ends in “equilibrium” or “crisis”, the following period begins “in equilibrium” or “in crisis”, and in such a case, it can more easily generate a dynamic of diverging disequilibria¹³.

1.1.2.3 Link with income distribution: In the period of the circuit a redistribution of income occurs. Money, initially created as income, is distributed and circulates between the social classes, which are the basic unit of analysis, in line with the classical tradition. Graziani thus radically rejects methodological individualism, which is the fundamental reason for his critique of the mainstream approach¹⁴. One of the indirect consequences of this macro viewpoint on distribution is that, by consolidating profits of the corporate sector, thus at the level of the capitalist class, these cancel out, and profit reveals its nature of mere transfer.

1.1.2.4 Causality from investment to saving: The circuit of Graziani retains the classical assumption that wages are paid in advance (Graziani, 1994), but despite this there is no pre-existing “wage fund”, which in the physiocrats and the classical economists was “corn” accumulated as savings from the previous periods. There is instead the creation of a monetary purchasing power made ex novo by banks, which reverses the causality between deposits and loans. This causality inversion was first noted by Schumpeter and Wicksell, then by the Treatise on Money of Keynes, which introduced the Keynesian circuit and has been largely followed by modern circuitists. If in an agricultural society it was necessary to first accumulate real savings (corn) to pay wages in advance, in an industrial society structured as a monetary economy this is no longer necessary. With money creation by banks, expenditures create savings, a quintessentially Keynesian as¹⁵. Indeed, the causality of loans on deposits corresponds logically to the causality of investment on saving.

1.1.2.5 Separation of banks from the rest of the private production sector: Another important logical contribution of Graziani’s circuit that he often emphasized, is the separation of private production by the corporate sector between banks, which produce money, and the non-banking corporate sector, which uses it¹⁶. Without this separation between banks and firms, it is difficult to integrate money into a macroeconomic model, a problem that concerns both neoclassical and neo-Keynesian analysis (including Patinkin). Graziani recalls that, whatever the reason for eventually holding liquid balances (payment or transaction), the complete reflux that occurs at the closing of the circuit in the case without crisis (total destruction of the liquidity created in the initial outflow or efflux that finances production) implies a null variation of liquid balances, a condition upon which Graziani builds a hypothesis of monetary equilibrium in the circuit. On the contrary, the constancy of liquid balances remains implicit in any classical or neoclassical macroeconomic treatment that, taking as a reference time period a span longer than that within which money is created and destroyed, abstracts from money itself. In this way, changes in monetary balances are excluded from the outset, thus transforming their nullity, which Graziani presents as a potential condition for equilibrium, into an identity¹⁷.

Without this breakdown of the private sector in terms of production and use of money, there can be no triangular money, that is, money in the circuit sense¹⁸, which, from the normative viewpoint, is also “seigniorage-free” money in the usual understanding of this term. In other words, when it exists, that is outside of the dynamics of equilibrium with unchanged liquidity, seigniorage can only be “private”, since there is no government or public sector in Graziani’s canonical model. As Riccardo Bellofiore has rightly pointed out on several occasions, this is one of the few points where Graziani’s circuit differs from that of Parguez¹⁹.

1.2 Graziani’s canonical model of the monetary circuit

Graziani developed several variants of the circuit based on specific assumptions. Here the model developed in chapters IV to VI of Graziani (2003a), which can be called “canonical”, is retained for presentation purposes. The model comprises one good, two financial products and three sectors: it thus assumes that the same good is consumed and invested and neglects the public and the foreign sectors²⁰. Households can only accumulate savings in the form of cash or securities, which, as noted, are liabilities issued respectively by banks and firms. These brilliant simplifying assumptions are the minimal ones necessary to integrate triangular money in a macroeconomic model, which could not be done if the productive sector were not broken down between banks and firms. They also show that, contrary to the mainstream monetary theory²¹, it is not necessary to introduce the Government to discuss the main aspects of money and finance, which concern the relations between firms and banks.

1.2.1 Presentation of the Model

As discussed, the circuit focuses on a single period that starts with the efflux phase, during which firms borrow from banks the liquidity the latter newly created and that is necessary to pay wages. Households, who are the third “pole” of the circuit, receive wages in exchange for their work in the production of consumer and capital goods. Initially, money created to pay wages represents an income, which is transformed into consumption and saving when consumption goods are sold to households. As for the Marxian reproduction scheme retained also by Kalecki (1942) in his theory of profits, consumer goods are sold by firms and bought by households at a market price that exceeds their production cost because the wage bill can only be spent on the purchase of consumer goods.

What happens during the single period of the circuit? Chapters V and VI of Graziani (2003a) give an answer in the fourteen equations presented in box 1 below²². On the left-hand side of each relation these set the value of an equal number of endogenous variables during a given period as a function, on the right-hand side, of these same fourteen variables and of nine variables that are exogenous, i.e. that are given during the period. Most of the exogenous variables reflect decisions taken by firms and banks. Of these, the crucial ones on the production side are the total level of employment N, the real rate of investment b, defined by firms, and wages w and productivity p, which implicitly assume a short-term horizon that can intuitively be taken to be the annual production cycle.

The level of employment N is determined by firms and validated by banks when they accept to grant them a loan. Given the wage level, it determines the initial money creation, which is thus endogenous. Given the production technology, which is assumed to be vertically integrated²³, together with N, firms and banks also set real output X, while, by defining the share of output allocated to real investment b and get it validated by banks, firms decide at the same time the proportion of workers they allocate to the production of consumer goods and capital goods. In the circuit, the decisions of households are thus subordinate to those of firms and banks, since the former decide both the level of production (via N) ²⁴ and that of the composition of output (via b), and through the latter, they set the price level (p).

As can be seen from the first equation in Figure 1, the allocation of output between consumption and investment (and of labour, since productivity is given), determines the price level, which is given by the product of a profit margin, given by the ratio between the propensity to consume and one minus the propensity to invest, multiplied by the sum of the unit cost of labour and firm’s debt. This price relationship is central because it shows that prices determine the distribution of incomes which, as Graziani notes, the circuit takes from Kalecki (1942). It implies that prices do not depend on the quantity of money, contrary to the monetarist viewpoint²⁵.

Figure 1: Macro-monetary and financial of Graziani’s canonical model of the circuit

It is worthwhile commenting upon the profit margin and the role it plays in the circuit in the sequence between initial and final finance, which, it can be reminded, is based on Graziani’s reading of Keynes’ finance motive (Graziani, 1984c and 1987) ²⁶. Mario Seccareccia (2004) emphasised the Wicksellian origins of Graziani’s circuit in his remarkable contribution to a volume in honour of Graziani that also contains several other analyses of the circuit of great interest. Wicksell’s ideas, for which reference is also made to Bellofiore (1998), influenced general equilibrium theorists such as Hayek and Lindbeck, but also the Keynes of the Treatise on Money, which, as Seccareccia shows and as Graziani (1981) also argued, is substantially consistent with the Keynes of the General Theory. Seccareccia also raised on several occasions an interesting objection to the fixed markup that appears in the price relation (1) that Graziani derives from the equality of aggregate supply and demand. For Seccareccia, in a genuine post-Keynesian model the markup should be variable and not fixed (Eichner, 1973) and, in particular, it should not be derived from a “Walrasian” equality between global supply and demand. While this objection is correct, it does not invalidate the fact that in the circuit, as in Sraffa’s analysis, distributive decisions are taken by enterprises and not by households. In fact, once the initial monetary value of production has been agreed with the banks, firms also determine and implicitly get banks’ validation for the other main variables of production and distribution, except for households’ saving and its allocation between bonds and liquid balances. It is, however, only the liquid savings of households that represent a problem for them, as they generate an equal amount of additional debt with the banking sector, which, in turn, results in a loss of real income because firms must use their profits to pay interest on bank’s loans, which is for them a real loss²⁷. Firms, on the other hand, are indifferent to household savings in the form of securities, since, by controlling both prices and distribution, they can pass the entire cost of interest on these securities back to households, setting prices to achieve the interest rate on bonds necessary to offset what banks offer on deposits.

This underlines an essential aspect of the circuit, which is that within the production period, starting with the creation and ending with the total destruction of money in the case without crisis, prices determine a redistribution of the initial allocation of the wage-value of production between consumption and investment, to what becomes at the time of final finance, the distribution of the value of the period’s product between wages, profits and interest²⁸.

Moreover, while it is correct that firms determine a markup that is fixed in the period between initial finance and final finance, because the length of the accounting period is in fact arbitrary, it can be made to tend to zero, allowing at the limit a continuous adjustment of the markup. Beyond this merely formal aspect, the point of substance remains that in Graziani’s model firms set both the level and composition of output and employment, which also set the markup for the period, they thus hold all the levers of decision. The fact that the markup is derived by equating global supply and demand, although compatible with Hayek or Walras, is mainly an application of Keynes’ concept of effective demand²⁹, because it is set at the beginning of the period as a function of expected demand. In fact, generalising on Kaleckian grounds the hypothesis of competitive markets accepted by Keynes, in Graziani’s model firms can set prices on an oligopolistic basis and have in practice the same capacity to determine prices and quantities as they would have in the case of a pure monopoly.

As Graziani (2003a, pp. 103-104) points out, it is clear from relations (7)-(9) on profits, that: (i) as in Kalecki, the rate of profit can be positive only when firms invest more than households save (b>s); (ii) monetary profits depend directly on the price level and increase with the interest rate that firms pay to households on securities i_B , which is in turn a function of i_L and i_D ; and (iii) real profits do not depend on the interest rate i_B that firms pay on the securities they sell to households, but, through the increase in prices, decline as a function of the interest rate paid to banks i_L which is paid out of their real income when all possibilities to increase i_B are exhausted. When the propensity to invest and the propensity to save coincide (b=s), the (excess-)profits cancel out and we are in the case of perfect competition. In the case of zero household savings (s=0), “capitalists earn what they spend while workers spend what they earn” ³⁰.

Relations (10) – (14) illustrate the formation of interest rates based on the equality between demand and supply of savings at the time of the circuit’s closure. Relation (10) ³¹ translates this equality under a reasonable assumption on the specification of the supply and demand for securities³² and, once verified, allows (12) to determine both the demand and supply of savings. (10) implies that for there to be equality between the supply and demand for savings, the interest rate i_B on securities issued by firms must be determined as a linear function of i_L with m and β given once the interest rate i_D paid by banks on deposits is fixed, but this level will not necessarily correspond to full employment (see below §1.3). If, in addition to this, it is assumed that all household savings are invested in securities issued by firms (b^d =1), there is also no change in liquid balances, a requirement that can be considered in a first approximation as a condition for the financial equilibrium of firms (Graziani, 2003a, p. 125) ³³.

The 14 endogenous variables: b^d, B, C, i_B, I_m, I_r, DL, p, P, P_r, r, S, X, Y, are determined by the relations (1)-(14) given the value of the exogenous variables, as summarised in the box in Figure 2 below. The exogenous³⁴ include two “structural” macroeconomic variables: productivity π and wages w. In addition to these, there are seven decision variables, of which two are determined by households: the savings rate s and the liquidity preference β. The others are determined by firms: the total employment N, the real propensity to invest b and the credit preference ratio of firms μ; and by banks: the interest rate paid by firms on loans i_L, and the interest rate paid by banks on deposits i_D.

Figure 2: Exogenous and endogenous variables during the period of the circuit 

1.2.2 A few numerical simulations

To illustrate the behaviour of Graziani’s model during the single period to which it refers, a number of comparative statics simulations are presented where virtual values are given to the exogenous variables and parameters that result in a central (or control”) solution for endogenous variables, which is then compared with that obtained by changing only one of the exogenous at a time. This second solution corresponds to a “partial derivative” of the system with respect to a change of a single exogenous near the central or “control” solution. The sensitivity illustrates the mechanics of the model, which is different from that of the neoclassical model. It does not claim to provide a realistic description of what would happen if in reality the exogenous variable changed as indicated. Indeed, the aim pursued here is not to use the model for the formulation of projections or scenarios, but to understand its properties. In more realistic simulations, other exogenous variables would move along with the exogenous considered and thus any alternative scenarios would have to calculate the effect of the change of several exogenous simultaneously (see the example in § 2.4).

1.2.2.1 Control simulation: Giving the following values to the exogenous variables and parameters results in the “control” values shown in the right-hand box for the endogenous variables³⁵:

Figura 3:Value of exogenous and endogenous variables in the reference solution

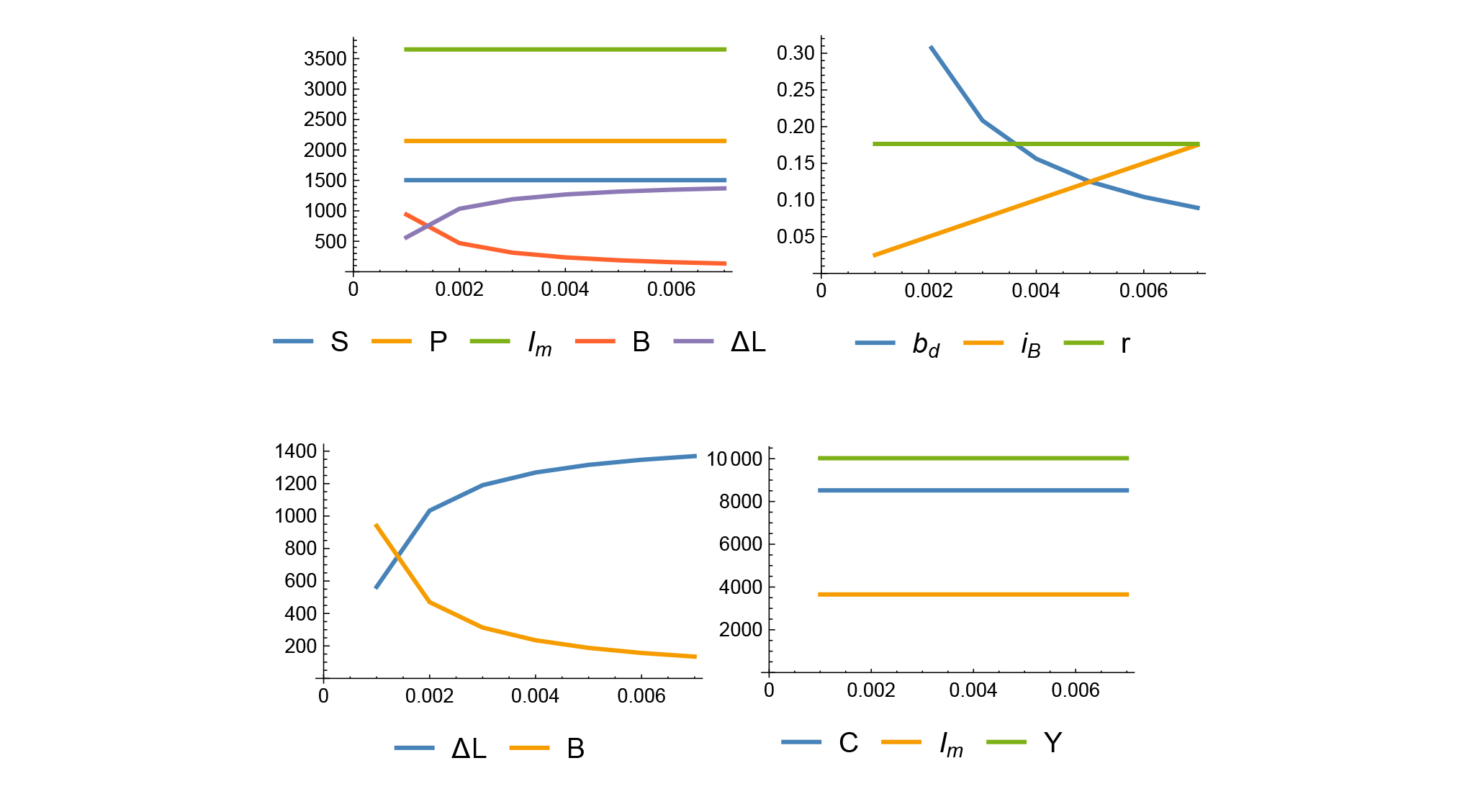
1.2.2.2 Exogenous variation of N: Starting from this reference solution, if total employment is varied between 700 and 1400, we can see in the three simulations described in the Chart 1 below that the distribution variables (S, P, I_m, B, L) increase proportionally while the main financial parameters (b^d, i_B, r) and in particular the rate of profit remain unchanged. The chart is not reproduced, but prices also remain unchanged, while, in the Keynesian logic of the circuit, both consumption and real household income increase due to the increase in activity.

Chart 1: Sensitivity to a change in the level of employment N decided by firms [700-1400].

1.2.2.3 Exogenous variation of b: The second simulation looks at the effect of a change of the real investment rate b between 0.2 and 0.5 and illustrates that this mainly influences the real profit rate and prices, which rise sharply.

Chart 2: Sensitivity to a change in the investment rate b [0.2-0.5]

Firms prefer self-financing to debt, especially debt coming from banks, therefore, to increase investment they first increase prices, which further increase both nominal profits and investment in monetary value. On the contrary, both real consumption and real household income contract after the price increase, because in this variant there are neither wage increases nor the increase in productivity that in a realistic scenario would be concomitant with an increase in investment. This confirms, however, that the mechanics of the model allow firms to finance an increase in investment through a decrease in real household income and consumption. Therefore, from an economic policy perspective, it is not enough to create the conditions for profits and investment to rise to increase real consumption and thus collective welfare: wages and productivity must also increase. In conclusion, b impacts on the price level, the rate of investment, the rate of profit and on firms’ self-financing rate, which rises from 29% to 82%.

1.2.2.4 Exogenous variation of s: Varying households’ savings rate s between 5% and 25% shows that savings, securities held, and cash balances increase, while nominal and real profits decrease because of the fall in prices and because the investment rate remains constant, while nominal investments decrease due to the fall in prices.

Chart 3: Sensitivity to a change in the savings rate s [5%-25%]

While nominal and real consumption remain constant, real income ultimately rises because of the fall in prices and the increase in savings, which inflates the wealth held in securities and, given the concomitant increase in liquidity, leads to greater indebtedness of companies to banks.

1.2.2.5 Exogenous Variation of π: By varying productivity π between 1.1 and 1.5, prices fall causing consumption and real income to increase. Conversely, the nominal and monetary variables remain constant.

Chart 4: Sensitivity to a change in the productivity rate π [1.1-1.5].

1.2.2.6 Exogenous variation of w: By varying the nominal wage w between 8 and 12 the first impact is felt on prices, which rise sharply.

Chart 5: Sensitivity to a change in wages w [8-12].

All nominal variables consequently increase, while financial parameters remain constant, as do consumption and real household income, for which the graphs are not reproduced.

1.2.2.7 Exogenous variation of μ: The effect of a change in the coefficient of firms’ preference for bank credit μ is examined by varying it between 0.2 and 0.6. In this case firms borrow more from banks at the expense of bonds B they issue to households. Since interest rates on loans are assumed to be constant, increased borrowing does not reduce nominal profits and investment if not marginally. The profit rate also remains constant, the interest rate on bonds slightly decreases, while the share of savings that households hold in the form of securities decreases. The reduction in the interest rate on corporate debt to households causes a small reduction in prices, which explains a slight reduction in the nominal variables (consumption, investment, and savings) that is undetectable in the chart. Consumption and investment fall in nominal terms, but in real terms both consumption and income remain constant (chart not reproduced).

Chart 6: Sensitivity to change in the coefficient of business preference for bank credit μ [0.2-0.6].

1.2.2.8 Exogenous Variation of b: Chart 7 looks at the impact of a change in the coefficient of liquidity preference of households β between 150 and 500.

Chart 7: Sensitivity to a change in the household liquidity coefficient b [300-500].

As the interest rate on deposits i_D and the interest rate on loans i_L remain constant, the interest rate paid by firms on their securities i_B only slightly increases, and the households’ demand for securities slightly decreases, while the profit rate does not change. Prices remain constant, as do nominal profits, savings, and investments, while, as mentioned, savings invested in securities decrease because of increased liquidity preference of households that obliges firms to request higher loans from banks. Real consumption and real income do not change, nor do their nominal levels.

1.2.2.9 Exogenous change in i_L: An increase of the interest rate set by banks on business loans i_L from 2% to 9% is considered.

Chart 8: Sensitivity to a change in the interest rate on banks’ loans to businesses i_L [2%-9%].

It can be seen from the charts above that, since the other exogenous monetary parameters (liquidity propensities of firms and households as well as interest rate on deposits) are assumed to be constant, the main effect of an increase of the interest rate on loans to firms is to increase firms’ supply of securities that compensates for the reduction in indebtedness to banks (DL), which they can achieve by increasing the interest offered on their securities. Through the price equation, firms neutralise any real effect so that neither household savings, profits nor monetary investments change substantially. Thus, there are also no real effects on household consumption and income because their nominal values are adjusted for inflation. However, due to the higher interest expenses, the total of their bond debt rises rapidly in proportion to the investment made (from 10% to 41% of the investment).

1.2.2.10 Exogenous change in i_D: Finally, an increase in the interest rate paid by banks on household deposits is considered, from 0.1% to 0.7%. This causes a reduction in the demand for securities and forces firms to raise the interest rate offered on securities, which, however, does not succeed in preventing an increase in household liquidity and, consequently, in their indebtedness to banks. Firms’ debt to banks rapidly rises in proportion to the investment made (from 15% to 37.5%). Neither nominal variables (savings, profits, investments, income, and consumption) nor prices change, so real consumption and income also remain unchanged.

Chart 9: Sensitivity to a change in the interest rate on banks’ deposits i_D [0.1%-0.7%].

1.3 The closure of the circuit and the double condition of real and financial equilibrium

At the end of Chapter VI, Graziani (2003a) notes that there are two equilibrium conditions in the circuit that determine the level of unemployment and that affect the model’s monetary variables and interest rates.

To see this, one can start from relation (10) which determines the interest rate on securities issued by firms i_B that, in conjunction with (12), allows them to recover the targeted proportion b^d of households savings, given the preferences of consumers for liquidity (β), those of firm for credit (μ) and the interest rates set by banks on deposits i_D and on loans to firms i_L. Relation (10) expresses a linear relationship between the interest that firms offer to savers on the securities they issue and the rate firms pay on loans from banks. Figure 4 below³⁶ illustrates this relationship which is a straight line in the Cartesian axes of abscissa i_L and ordinate i_B. The line with a slope of β₁ (blue line) corresponds to the initial equilibrium of the capital market. By setting the additional condition b^d=1, one can calculate the (i_B, i_L) pair value such that all household savings will be invested in securities, which occurs at point C. Point C maintains the constancy of liquid balances held by households, and therefore a stable quantity of money—a hypothesis which, as Graziani notes, was also adopted by Keynes in the General Theory. This implies an unchanged level of corporate indebtedness to banks, which can be interpreted as a condition for the dynamic financial equilibrium of firms. For the sake of the argument, point C can also be assumed to reflect initially full employment conditions.

With the parameters considered in Figure 4, this favourable combination of circumstances is realised when banks set the interest rate i_L on loans at 8% at point C in Figure 4. In this case, firms will set the rate they pay on securities held by households at i_B =4%. As noted, point C ensures the constancy of liquid balances because of the values chosen for the interest rates’ pair and it is by assumption a position of full employment that would logically incentivise firms to maintain full employment also in the following period, given their unchanged debt. If, however, during the production period the liquidity preference coefficient increases from β₁ to β₂, the line representing capital market equilibrium shifts upward (orange line). In this case, if banks keep their loan rate i_L steady at 8%, the new rate on securities i_B will settle at 5% (point C’), a level insufficient for firms to absorb all savings. It is therefore plausible that, at the beginning of the following period, firms, having seen their debt rising in proportion to total investment, may reduce production and employment due to the loss originating from the real income transfer to the banks. Indeed, due to the increased preference for liquidity, the demand for securities decreases. For liquid balances to remain unchanged, banks would need to set a higher interest rate on loans i_L at 10%, based on which firms would offer a rate of i_B at 6.25% on their securities. The point at which all savings are absorbed by firms’ securities has thus shifted from C to D, whereas if it had remained at C’, it would probably have implied a reduction in employment.

Figure 4: Dynamics of a change in liquidity preference.

The circuit thus shows that there are two conditions for full employment of which traditional Keynesian economics only considers the first: i) the interest rate and the level of investment must allow for full employment, as Keynesian models usually require; ii) there must also be a financial equilibrium between banks and firms to prevent unemployment, a fact that cannot be made explicit unless the private sector is split in two by isolating banks (Graziani, 2003a p. 128)³⁷. This explains why full employment is extremely unstable when a sequence of individual time periods is considered. Graziani’s view of dynamics is, as in Kalecki (1954), that of a succession of short-term imbalances in which the “Malthusian” case that arises when the circuit is closed “with crisis” prevails.

2. Empirical relevance of the monetary circuit

In this section, past results are reported that were so far unpublished and some more recent data is examined on the development of macro-financial aggregates linked to the empirical relevance of the circuit. Graziani’s canonical model of the circuit is then simulated to offer a possible explanation of the trends observed.

2.1 A study of 2008

In 2008, the EIB Institute financed a study at the University of Nice in which the monetary circuit theory was empirically tested on the Visegrad countries (Czech Republic, Slovak Republic, Slovenia, and Hungary) and Turkey with the econometric tools in vogue at the time. The research confirmed the validity of the monetary circuit. Five hypotheses were subjected to econometric estimation for the Visegrad countries, and the results are summarised in the box below.

Figure 5: Summary of the 2008 Starebei study.

Based on this experience, it can be said that one of the difficulties of empirical tests on the money circuit is that initial finance is not observed (see also section 2.3). In some respects, one could say that initial finance is the wage bill, in other that it is GDP, i.e. (approximately) the sum of labour and capital income, although both aggregates in national accounts are observed at the closure of the accounting period. They are thus calculated at market prices and relate to final finance. There is no observable variable that corresponds exactly to the concept of initial finance. It would therefore be necessary to look at the macroeconomic aggregates at factor costs and better integrate what is called the data-generating process into the econometric estimates (Hendry & Richard [1983] 1993).

2.2 Money creation and the dynamics of wages and financial wealth³⁸

Being non-neutral most of the time, by definition the endogenous money of the circuit can affect relative prices. In particular, the possibility to finance speculation by monetary creation may be a reason for the faster growth of the market value of financial assets in the circuit of accumulated savings (financial circulation or circuit of capital), compared to that of assets consumed in the generation of current income and in particular wages (industrial circulation or circuit of income).

Once one accepts the definition of money as a “third-party” liability issued by banks to allow payments to be made (Schneider, 1962), one also understands that deposit money that is created at the time of lending and is destroyed when the loan is repaid can be lent in the meantime to finance the purchase and sale of real assets and financial securities and thus influence their price. Moreover, outside the simplified framework of the canonical circuit model, within the production period money can also be created by banks to purchase securities, and thus potentially play a speculative role³⁹. At the cost of a small logical leap that should be made explicit, the circuit can thus illustrate and explain financialization, which, while being a debatable concept that requires clarification (Toporowski & Mitchell, 2013 & 2014), remains one of the most conspicuous macro-financial phenomena of recent decades.

The following graphs illustrate the divergent developments in the relative prices of financial assets and income-creating flows, the so-called asset price inflation (Toporowski, 2000) and can be interpreted from a circuitist perspective.

Chart 10: Wages, interest, and financial assets USA 1954-2016.

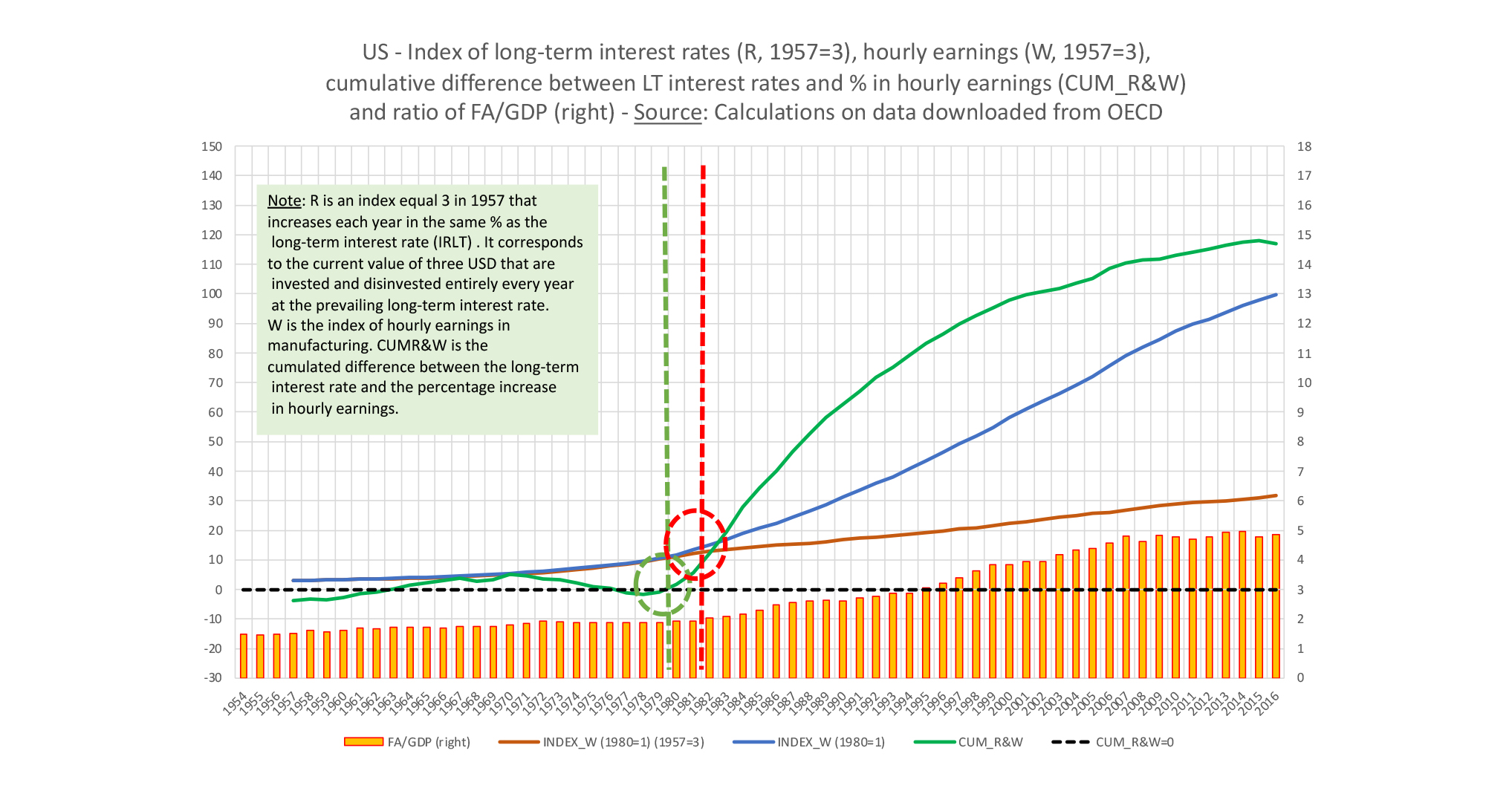
If we take the US case in Chart 10 as an example, comparing the long-term evolution of a basket indexed on wages and a basket indexed on the price of financial assets we see that the wage index has permanently lost ground to the financial index. If a worker had 3 USD in 1957⁴⁰ and invested them in an index that had advanced at the same rate as the value of wages in the US manufacturing industry (brown line), he would have 32 USD in 2016. If, on the other hand, he had invested it in an index that had behaved like the US long-term bond index, he would have had 100 USD in capital in 2016 (blue line). The divergence between the blue and brown curves starts in 1979-1980, as confirmed by the evolution of the green line, which illustrates the cumulated difference between them, and which becomes positive after 1982. The columns in yellow, on the other hand, represent the evolution of the ratio of financial assets to GDP in the United States, which went from a value of less than two before the 1980s to a value of around five in 2016. Financialisation thus manifests itself in the form of an increase in the value of financial stocks relative to production flows, reflecting a negative evolution of the relative price of labour. The same kind of evolution can be observed in the graph below for the UK, but during different time periods that can however be interpreted in the same way.

Chart 11: Wages, interest, and financial assets UK 1960-2016.

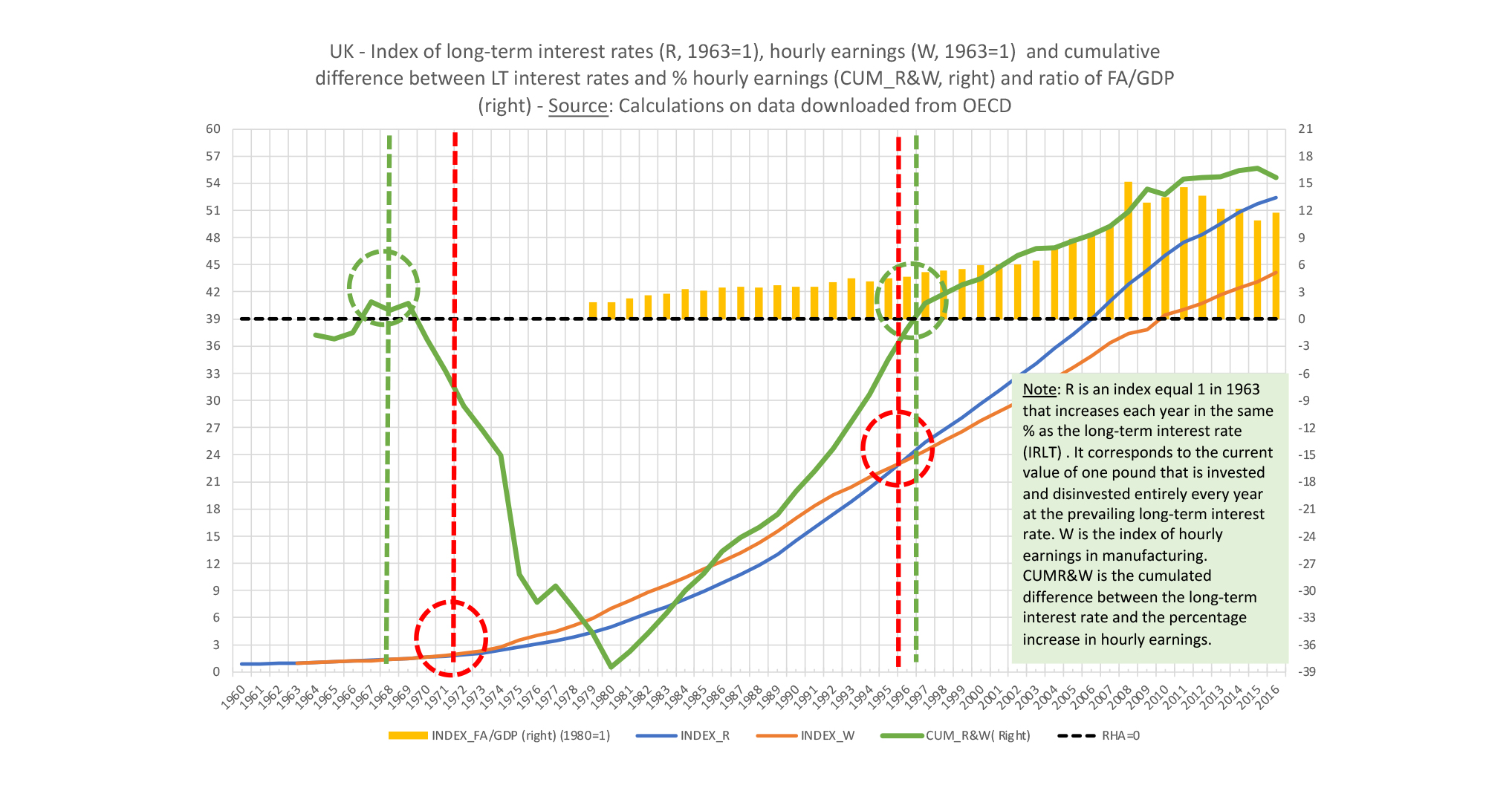
If one took an index equal to one UK pound (GBP) in 1963 that had grown like the hourly wages in the British manufacturing sector (brown line), this would have reached a nominal value of 46 GBP in 2016, as shown in Chart 11. The same pound in 1963, invested instead in an index that had risen like the long-term rate on UK government bonds (blue line in the graph), would have come to be worth 54 GBP in 2016. The accumulated divergence between the two indices (green line) remained negative (i.e. favourable to wages) between 1970 and 1996 and reached its lowest point in 1982, from which year it began to recover to become positive in 1996 and reach a value of around 16 in 2016. For the period for which data are available, which begins in 1979, the ratio of financial assets to GDP which was 1.85 in 1979 increased to 3.6 in 1991, rose to 15.1 in 2008 and then fell to 11.7 in 2016.

Chart 12: Wages, interest, and financial assets EZ 1973-2016.

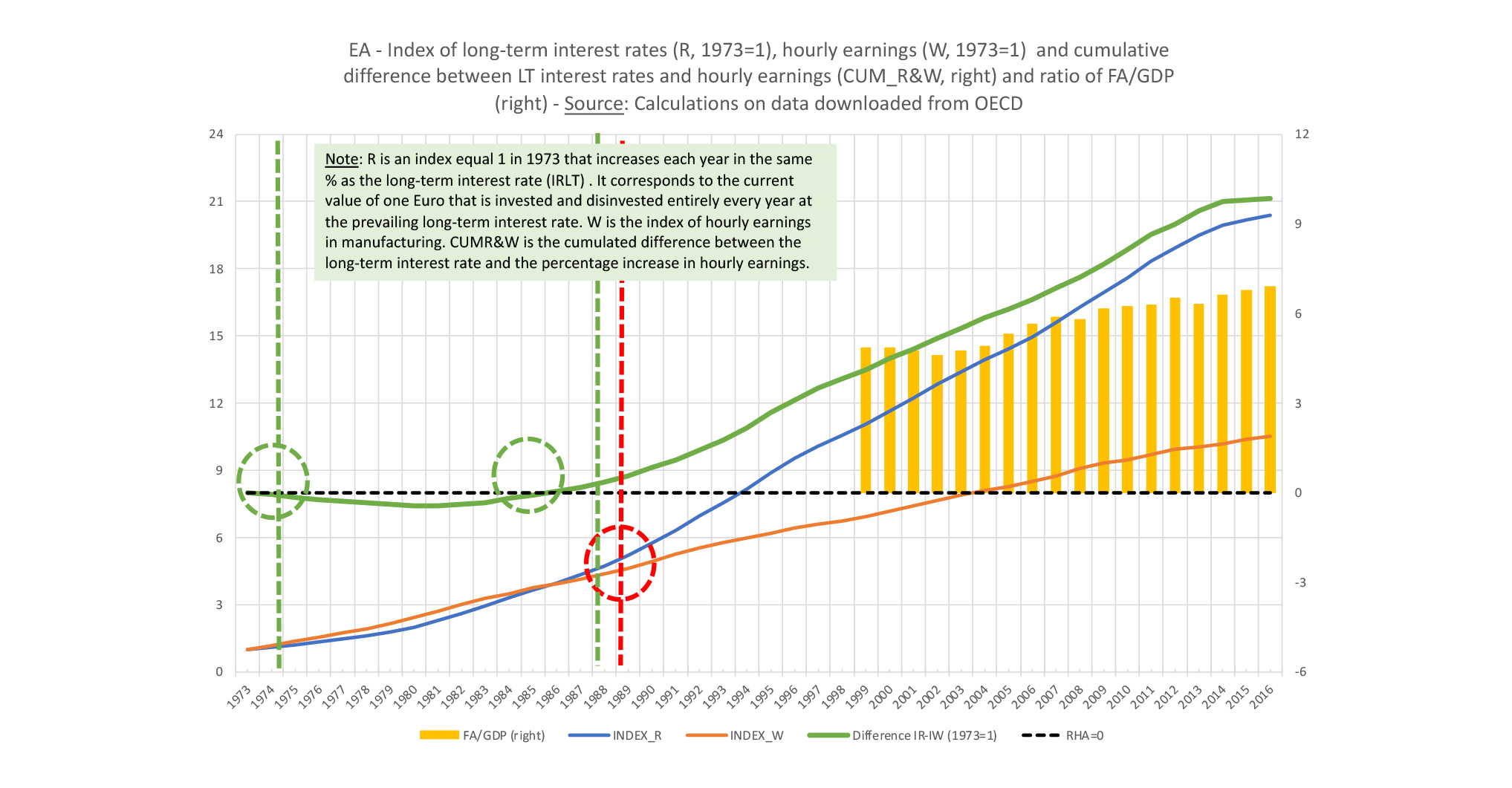
Finally, also with regard to the Eurozone, the data of Chart 12 indicate that a Euro from 1973, invested in an index that had grown like hourly wages in the manufacturing sector (brown line), would have reached a nominal value of 11 Euros in 2016. The same Euro, invested in long-term bonds, would have reached a nominal value of 20 Euros in 2016 (blue line). The accumulated divergence between the two indices (green line) remained in negative territory from 1973 to 1986 before exceeding 10% in 1989 and reaching 48% in 2016. The ratio of financial assets to GDP, which was 4.83 in 1999, rose to 6.88 in 2016.

The unfavourable evolution of the relative price of labour compared to that of financial assets such as long-term bonds documented in the previous graphs is confirmed when examining other forms of savings’ allocation as done in Chart 13 below which examines the evolution of the relative prices of various financial and real assets for the UK by comparing the nominal value of these assets in 2015 to what they were in 1995⁴¹.

Chart 13: Comparison of different financial indices for the UK 1995-2015.

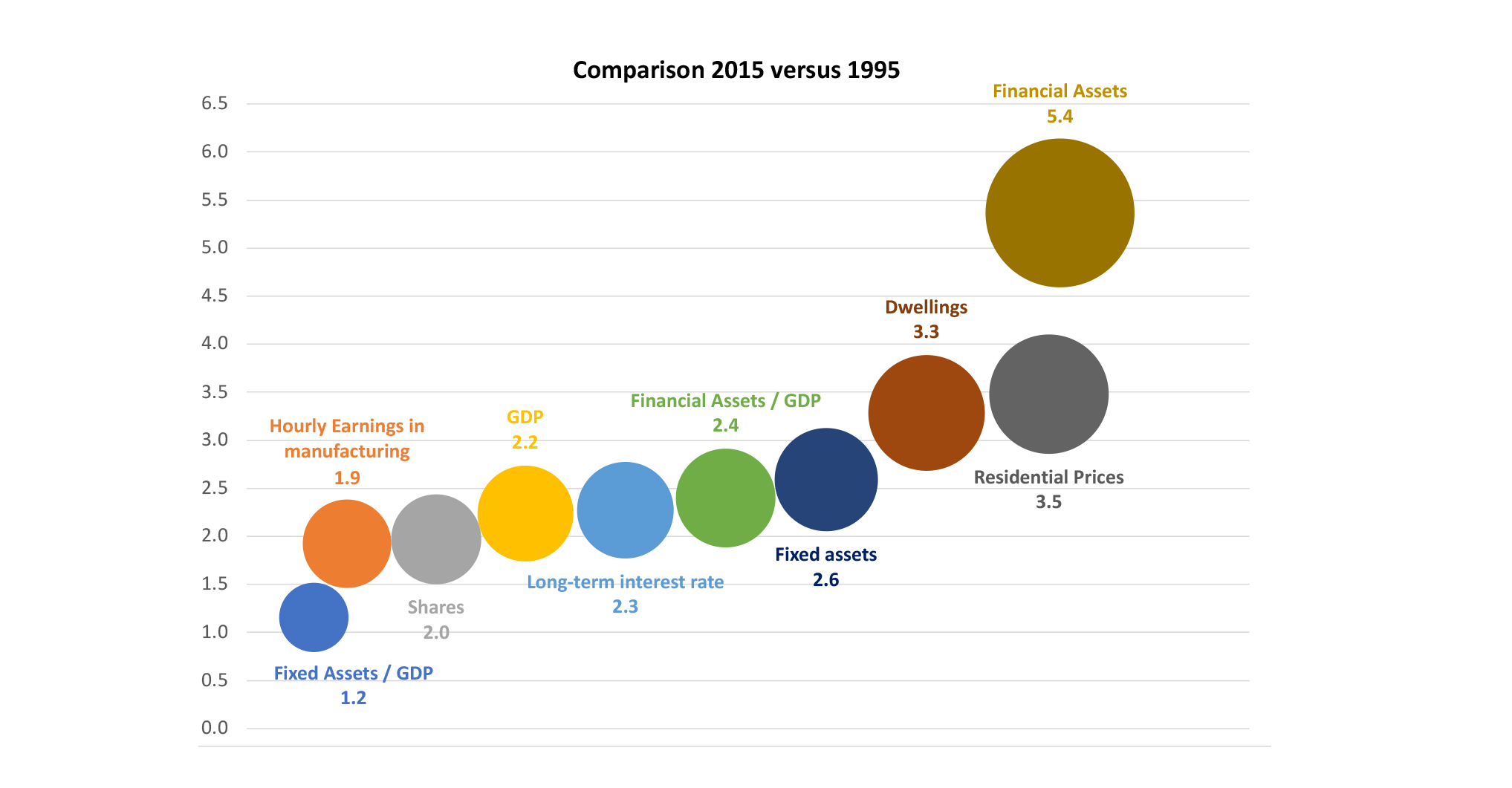
It can be seen in this chart that during the period examined the value of total financial assets was multiplied by 5.4, while that of the residential price index was multiplied by 3.5, that of fixed assets (real investment) by 2.6, that of long-term bonds by 2.3 and that of shares by 2.0. In comparison, the index based on nominal GDP takes a value in 2015 that is 2.2 times that of 1995 and for that of hourly wages this ratio is 1.9. It can thus be seen that the growth in the value of financial assets has been much faster than the growth in the value of flows related to current production. In particular, financial assets have grown faster than GDP. Their value has more than doubled relative to GDP (2.2). In contrast, for fixed assets, indicative of the evolution of the value of ‘real’ investment, this ratio is 1.2. Nominal wages, on the other hand, grew less rapidly than GDP over the same period, so that they lost even more than the latter to financial assets.

These graphs document how, over the past decades, there has been a parallel increase in the weight of financial assets in relation to GDP and an unfavourable evolution of income distribution at the expense of labour. This is not the place to go into the details of these trends, but the substance is quite intuitive: if one admits that banks or the financial system as a whole can create liquidity (and/or quasi-liquidity) based on their speculative bets, effectively without limits, it is logical that this liquidity will be directed towards higher-yielding and less risky assets. If, moreover, the system allows a constant inflow of new liquidity to the financial markets (Toporowski, 2000, pp. 31-41), the conditions can be created for self-fulfilling expectations of permanent increases in capital gains that exceed any return offered by traditional accumulation.

2.3 A look at more recent macro-financial aggregates

To complete the empirical picture, this section examines more recent data for the Euro Zone. As argued above, the difficulty for the empirical evaluation of the circuit is that initial finance is not observed⁴². Various aspects of final finance are observed instead, particularly for debt and liquidity accumulated at the end of the period, as well for savings. The interesting point to examine is obviously that of the causality of loans over deposits. As already mentioned, from this viewpoint, the purchase of a security by banks has the same effect of a loan, i.e. it creates money, but without necessarily creating income, and this may help to explain the observed trends of the financialisation process⁴³. Banks, and more generally the financial system, by buying and selling securities within the circuit of savings, can therefore increase their price (in financial circulation), leading to an increase in the value of assets accumulated in the past compared to current production values (in industrial circulation). Some charts to the most recent period allow a quick indirect check of this and other main ideas of the circuit. The first graph on the left of Chart 14 below shows GDP and the value of loans on the assets side of the euro area’s financial and monetary intermediaries. A certain correspondence can be seen between the two series. The figure on the right shows the absolute changes in the same variables, and here too there is some correspondence, although it is not perfect.

Chart 14: Euro area – Loans and nominal GDP: level (left) and change (right) 1990_Q1-2021_Q1

The graph on the left in Chart 15 below concerns liabilities issued by enterprises in the form of both loans and securities and compares them to aggregate wages over the last 15 years⁴⁴. Highlighted are two sub-periods in which the reduction of loans taken out by firms led to a deceleration of wages. In the graph on the right in Chart 15, which plots loans and securities purchases on the assets side of Eurozone banks in both stock and absolute change terms, it can be seen that the evolution of securities held, and loans have been fairly correlated, whether in levels or in changes.

Chart 15: Eurozone – Corporate debt (left) and bank loans (right) 1990_Q1-2021_Q1

It is noteworthy that the ratio of flows to stocks has been declining over time, as can be seen in Chart 16 below, which depicts the evolution of debt to liabilities of firms: loans (F4) in blue and securities (F3) in orange, both expressed as a percentage of the stock value.

Chart 16: Eurozone – Corporate debt: ratio of flows to stocks: 1990_Q1-2021_Q1

It can first be observed that this percentage is low: since 1999, the value of money borrowed during the year was of the order of two per cent compared to the value of accumulated debts and loans and it fell to one per cent in the years after 2009. Thus, a reduction in the value of flows relative to stocks can be observed over time, which implies an increase in the relative price of financial assets representing accumulated wealth relative to flows such as wages.

Chart 17: Eurozone – Deposits of households and firms as % of GDP: 1990_Q1-2021_Q1

This last aspect is confirmed in Chart 17 on the left, which shows that the ratio of deposits to GDP for Euro area households and firms has increased almost steadily over the last 25 years, by about one percent of GDP for households and 0.5 percentage points of GDP for firms. The hypothesis of no changes in liquid balances is therefore not empirically verified, indirectly confirming the relevance of the circuit’s explanation for the parallel reduction in activity and increase in asset prices (cf. §1.1.2.2 and §1.1.2.5).

2.4 Financialisation and the canonical model of the circuit

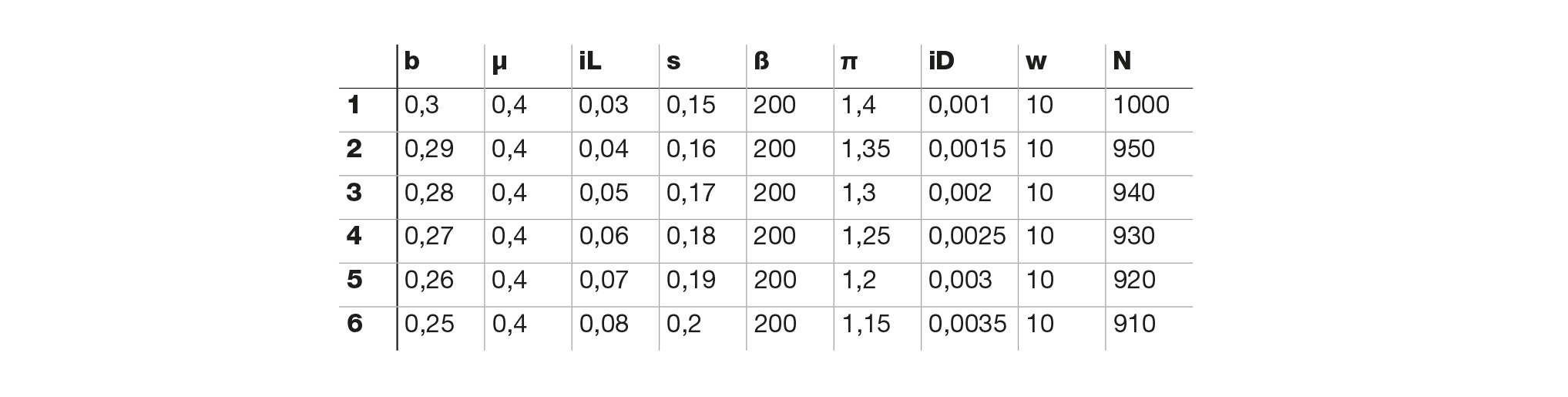
Graziani’s circuit describes a monetary production economy that includes the essential aspects of finance, particularly the accumulation of money and capital, yet it remains a flow model. To thoroughly address the topic of financialization, it would be necessary to add to the “block” in Figure 1 other relationships that reflect the behavior of accumulated stocks and their prices from the closure of the first period of the circuit’s onward. Nonetheless, even without these modifications, the model can replicate various aspects of financialization in a comparative statics exercise, that is, within the context of a recursive single-period equilibrium. This result can be shown by constructing a scenario for the model’s endogenous variables, combining some of the changes in the exogenous variables examined individually in §1.2.2. This scenario simulates an increase in financial rents by introducing a rise in exogenous interest rates i_D and i_L, which in turn also raises the endogenous interest rate on bonds i_B⁴⁵. In this context, one can also assume a parallel increase in the saving rate s. In light of the argument in §1.3, the increase in financial rent has real effects in the periods following the first, which can be introduced by progressively reducing the exogenous parameters of real investment rate and employment⁴⁶, while one can assume that reduced investment would also tend to lower productiviy. The idea, therefore, is to start from the control solution in §1.2.2.1 and examine six subsequent periods in which the exogenous variables of the model in Figure 1 take on the respective values given in Figure 6.

Figure 6: Financialisation scenario: assumptions on exogenous variables

The results of the simulation are illustrated in the charts of Figure 18. The first chart shows that interest as a percentage of households’ income rises from 0.4% to 1.9%, while the second chart illustrates that the liquidity variation increases from 9% to 14% of income.

Chart 18: Financialisation scenario: results on endogenous variables

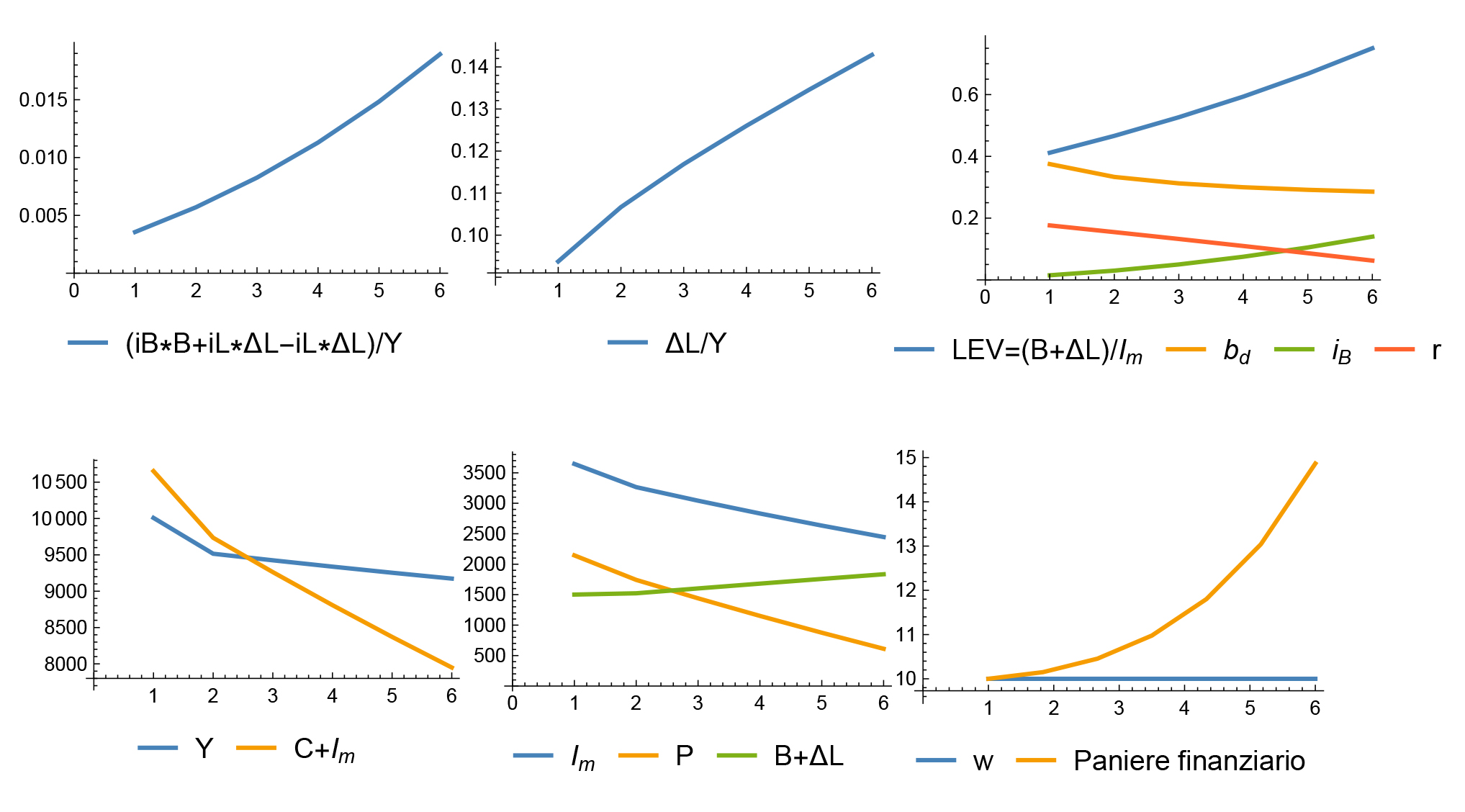
In the third chart, we see that leverage, defined as the ratio of the sum of the increase in corporate debt to banks DL and households B divided by nominal investment, rises from 41% to 75%, despite the reduction in the household demand for securities b^d. The profit rate has obviously fallen, as b has decreased and s has remained constant. As seen in the fourth chart, the scenario is also characterized by a trend of decreasing household income and final demand at nominal prices, along with substantial stagnation of income and consumption in real terms (chart not shown). The fifth chart shows that nominal investment declines, with profits representing an increasingly smaller share, the balance being covered by the sum of debt to banks (ΔL) and households (B). Finally, the last chart illustrates that in terms of income distribution, a basket of goods initially equal to the nominal wage of ten, but invested in a financial index growing at the speed of the interest rate on firms’ securities, would have reached a value of fifteen after six periods, while, by assumption, the wage was fixed at ten and remained unchanged.

In conclusion, the econometric tests conducted in 2008 for the Visegrad countries empirically validated the theory of the monetary circuit for these countries, which was not entirely obvious a priori, given that these were at the time and perhaps are still today economies in transition. Moreover, given that what differentiates the circuit from mainstream approaches is the addition of a third banking pole that creates money autonomously according to the profitability of the discounted liquidity flows of the various possible investments⁴⁷, the indicators examined confirmed that the monetary circuit theory is useful for understanding the main recent macro-financial developments and in particular the fall in the relative price of labour relative to that of long-term savings, one of the most significant developments of the financialisation era. This can be explained by the fact that leveraged finance increases the value of financial stocks more than production-related flows such as wages, less attractive at the stage of initial finance.

3. The link with the theory of value

In addition to its theoretical interest discussed in the first part and its practical ability to describe and explain a number of empirical facts, discussed in the second part, the interest of the circuit is also to provide a link to the theory of value, which, as in Keynes’ General Theory, is a value expressed in units of wages (Graziani, 1983b), a point emphasised several times by Bellofiore (1989, 2018). It is briefly argued in this last section that this link can be used to construct a “heterodox” cost-benefit analysis, since the non-neutrality of circuitist money also implies a logical distinction between accounting prices, to be used to assess the social impact of financed investments, and market prices, expressed in cash.

Taking the neoclassical result of Allais’ (1943, 1981) rendement social as correct (as it is), the change in welfare associated with a change in the economy is essentially given by the product of the “incremental” quantities ΔQ for an “accounting” price P_A:

For Allais, this price is the market price, which is assumed to be the same as the neoclassical equilibrium price in a market economy⁴⁸ut in other approaches it can be different. For example, endogenous money, which is most of the time non-neutral in the circuit, leads to a rejection of the idea that neoclassical equilibrium relative prices can be market prices⁴⁹. ΔQ is instead an empirical “fact” to be ascertained on a case-by-case basis.

The problem for socio-economic evaluation is in how one calculates P_A. The circuit is based on the temporal and instantaneous equality between the value V(X_t) of the production X_t realised in a period of time and the value of the monetary incomes created to remunerate the labour employed for this purpose at the beginning of this period. There is thus a temporal correspondence between the money flow created at time t for productive purposes DM_t and the ‘social’ value V of the goods produced during that period:

a relationship that resembles that of the quantity theory of money but has a completely different interpretation, as it refers specifically to the income-money created at the beginning of the period (initial finance) rather than to the stock of money accumulated at the end of the period or to its variation (part of final finance). Incidentally, this also shows the logical link between money and net investment, since, like money, investment is created and accumulated within the circuit period and is therefore both a flow and a change in stock.

Although there are not many theoretical or empirical studies that address the issue from this point of view, one can take as a starting point the work of Vallageas (1976, 2010, 2018), which proposes to correct “market production prices”, for the fact that profits, in Schmitt’s interpretation to which Vallageas refers in this respect, are a pure transfer. The “wage-value” accounting that he develops has the effect of correcting market prices and transforming them into prices expressed in “labour-value” and thus opens a path that in some respects reconnects with Lesourne’s (1977) expressed wish to develop a cost-benefit analysis expressed solely in terms of time-value and that also offers suggestive links with the classical labour-value theory⁵⁰. In fact, once the link between the value of money created for current production and the value of money financing the purchase of real and financial assets existing during the same period has been better clarified (cf. discussion in part 2), a work that remains largely to be developed, one can think about integrating the circuit with the interpretation of the labour-value theory accepted by Pasinetti (Pasinetti & Garbellini, 2015). This line of enquiry promises to be difficult and laborious, but it is very interesting and potentially fruitful in terms of useful results. It can also make good use of the reflection that Riccardo Bellofiore (1989, 2018) started some time ago on these issues.

Conclusion

In the model of the monetary circuit:

1. Banks and money have their own existence and proper function. The model is particularly suited to interpret realistically monetary phenomena related to new lending or borrowing.
2. There is a macroeconomic foundation of microeconomics. “Loans create deposits” and other related propositions involving alternative causal chains to assess the effects of monetary and financial economic policy are verified and/or empirically verifiable. The model can also be used to explain the formation of financial rents.
3. Central to the analysis is the link between loans, money, investment and income distribution, which is crucial for understanding the social effects of economic policy. It is known that, out of the neoclassical equilibrium, allocation and distribution are not independent, which requires an economic approach to the distribution problem that is open to multidisciplinary analyses explaining its extra-economic aspects (Roncaglia, 2024). To this end, the circuit suggests the use of frameworks based on labour-value theory to assess the social effect of banking operations.
4. In the version developed by Graziani in an autonomous and original manner⁵¹, the circuit is compatible with that of the other authors who were the founders of the approach, namely Schmitt, Parguez and Poulon, who complete his analyses with results that are complementary from the policy viewpoint.

In conclusion, the monetary circuit appears inescapable for assessing the economic and social effects of banking and it is therefore undoubtedly a useful scheme that needs to be deepened and developed. It remains one of Augusto Graziani’s most original and fruitful contributions.

A short closing remark is due on how the circuit relates to the rest of his rich scientific and cultural work. Graziani was a “complete” general economist with a penchant for macroeconomics and a great expert on money and monetary policy. He tackled all the most difficult problems in economic theory armed with his great culture and profound knowledge of the history of economic thought, nourished by his careful reading of economic classics in the original language. From the very beginning of his long teaching career, he was interested in the problems of cost-benefit analysis (Graziani, 1961) well in advance of the first manuals that the OECD and the World Bank would devote to the subject at the end of the 1960s, progressively restricting it to the neoclassical sphere. His intellectual rigour led him to reject the neoclassical analysis of capital as early as 1965, indirectly and discreetly contributing to an important and generally neglected debate involving the leading neo-Keynesian and post-Keynesian economists of the time on both sides of the Atlantic (Graziani, 1965, discussed in Cingolani, 2016).

But his fertile creativity was not devoted only to theoretical issues. In addition to educating several generations of students, many of whom went on to become teachers or managers in Italy and abroad, he paid great attention to history (Graziani, 1975) and was a citizen strongly engaged in the political and civil debate. In particular, he dedicated much of his energy to address concretely the difficult problems of the development of the Italian Mezzogiorno (Graziani, 2020), animating among other things, together with Rossi, the famous Portici School (Costabile, 2004), which contributed to forming a significant part of the national economic ruling class.

It is probably from the confrontation between his careful observation of reality in its most difficult facets and his profound knowledge of the economic doctrine that the intuition of the monetary circuit was born. As this text tried to show, this scheme offers a simple and rigorous tool for reasoning about monetary and financial issues, which is empirically relevant and rich of future development perspectives.