La prima parte di questo contributo ricorda la definizione di moneta endogena data dal circuito monetario1 e accolta da Augusto Graziani, per poi descrivere quello che si potrebbe chiamare il “modello canonico” della versione del circuito da lui sviluppata, che fornisce una descrizione succinta del funzionamento di una macroeconomia che integra pienamente la moneta e le banche. La seconda accenna ad alcuni riscontri empirici del circuito monetario. Volgendo lo sguardo ai possibili sviluppi futuri, la terza parte presenta alcune idee sul possibile utilizzo della teoria del circuito monetario per la valutazione sociale delle operazioni bancarie.
1. Un po’ di teoria
Le operazioni bancarie sono un tipo particolare di operazioni finanziarie, e come scrisse de Finetti:
“Le operazioni finanziarie si riducono a scambi di denaro; a volerle considerare nella loro accezione più larga possibile, potremo anzi definire appunto le operazioni finanziarie come quei contratti di scambio in cui non figura nessuna merce fuorché il denaro”, De Finetti (1935, p. 471).2
Per valutare gli scopi dell’attività bancaria dal punto di vista dell’utilità collettiva bisogna quindi ragionare su uno schema che integri pienamente la moneta e le banche e spieghi come queste si relazionano col resto del sistema economico e sociale. Il circuito monetario di Graziani soddisfa questi due requisiti e si differenzia in questo da molti approcci mainstream3. Come ricordato da Riccardo Bellofiore (2022), il circuito di Graziani è un modello economico a due beni (consumo e investimento) e a tre settori o poli istituzionali: le famiglie4, le banche e le imprese. In questo schema logico la moneta si definisce come una passività emessa dal settore bancario, che viene utilizzata come mezzo di pagamento fra famiglie e imprese proprio perché estranea alle loro transazioni (definizione triangolare della moneta). Il ruolo specifico della banca in questo contesto è quello di produrre mezzi di pagamento emettendo una passività “liquida” creata contestualmente all’atto di consentire un credito, un attivo di bilancio che non è liquido, a differenza del passivo monetario corrispondente5.
1.1.1 La dimensione “sistemica” del circuito di Graziani
All’interno del sistema economico, l’attenzione di Graziani si focalizza sulle variabili monetarie a cui dedica un’analisi dettagliata, sviluppando di fatto il nocciolo di quello che si può indicare in gergo come il “blocco monetario e finanziario” di un modello macroeconomico6. In linea di principio, questa scelta rende possibile l’uso del circuito monetario in modelli con interpretazioni economiche diverse, perché il blocco di equazioni che spiega le variabili monetarie può essere integrato in schemi che possono spaziare, al limite, dai modelli neoclassici di breve termine ai modelli di lungo termine alla Garegnani o alla Pasinetti7.
Ma pur concentrandosi sul fenomeno monetario, l’analisi non perde di vista l’aspetto sistemico. Post-Keynesiani come Eichner (1991) o Mockers (2016), ma anche molta dell’economia classica e neoclassica e in particolare i modelli di Leontief, hanno recepito l’idea di applicare la teoria dei sistemi all’economia. Può essere anche utile ricordare a riguardo che la letteratura francese, che Graziani conosceva molto bene, ha da tempo identificato il carattere sistemico del circuito e in particolare Poulon (2015, pp. 9-94), uno dei fondatori del circuito, va fino ad opporre il “paradigma sistemico” del circuito a quello “insiemistico” dell’equilibrio generale8.
Si può senz’altro dire di Graziani che, pur sviluppando principalmente l’analisi del settore monetario e finanziario, ragiona in una logica macroeconomica di sistema. Di fatto, una delle sue conclusioni più keynesiane, ripetuta in vari scritti (in particolare 2003b), è che, proprio a causa dell’integrazione della moneta, si crea un effetto sistemico per cui il tutto non è più la somma delle parti9. La moneta è cioè un elemento che spiega la “fallacia della composizione” messa in luce dall’analisi keynesiana10.
1.1.2 Caratteristiche della moneta circuitista
È utile ricordare alcune caratteristiche della moneta nel circuito di Augusto Graziani.
1.1.2.1 Sequenzialità: Si tratta in primo luogo di una moneta inserita in una dinamica temporale all’interno della quale è creata, circola, e viene accumulata o distrutta in uno scambio triangolare fra banche, imprese e famiglie (cf. §1.1.2.5). Quest’analisi dinamica si esplica in una sequenza di fasi (§1.1.2.2) e periodi che si susseguono nel tempo storico. In questo, il circuito di Graziani è diverso dal circuito di Schmitt (1984), che si svolge nel cosiddetto tempo quantico, ed è invece molto vicino a quello di Alain Parguez (1996 e 2000 con Seccareccia) e di Poulon (2015). Una delle conseguenze di questa sequenzialità è che il circuito permette un’analisi causale che è per lo più esclusa dai modelli simultanei. Questo è rilevante ai fini di politica economica, poiché a rigore la causalità è una premessa necessaria per discutere l’effetto di uno strumento di politica economica (variabile che si vorrebbe idealmente esogena) su una variabile obiettivo (considerata usualmente endogena) 11.
1.1.2.2 Enfasi sul periodo singolo: Come altri esponenti del circuito (Schmitt, Parguez e Poulon), anche Graziani, pur interessandosi primariamente alla dinamica monetaria, concentra la sua analisi su un singolo periodo, che sceglie essere quello iniziale (o “all’origine dei tempi”), e lo scompone nelle sue fasi temporali, anch’esse sequenziali. In questa successione di fasi la moneta è prima creata e poi circola, trasformandosi in reddito e in seguito in consumo e risparmio. Al termine di questo periodo la moneta è accumulata o distrutta. Questa sequenza temporale rivela la duplice natura di flusso e di stock della moneta endogena del circuito (Graziani, 1996 e 2002). Al termine del singolo periodo, se tutta la moneta creata inizialmente è distrutta, si ha una situazione di equilibrio, descritta nell’articolo del 1984 su Moneta Senza Crisi (Graziani 1984b). Altrimenti, si ha una situazione di “crisi” descritta nell’introduzione al libro del 1980 della Costabile su Malthus12. In entrambi i casi, al singolo periodo iniziale fanno seguito altri periodi. A seconda che il primo periodo sia finito in equilibrio o in crisi, il periodo successivo comincia in equilibrio o in crisi e può quindi generare più facilmente una dinamica “dello squilibrio”13.
1.1.2.3 Legame con la distribuzione dei redditi: Nel periodo del circuito avviene una redistribuzione dei redditi. La moneta, inizialmente creata come reddito, viene distribuita e circola fra le classi sociali che, come per gli economisti classici, costituiscono l’unità di base dell’analisi. C’è quindi in Graziani un rifiuto radicale dell’individualismo metodologico, che è la ragione fondamentale della sua critica all’approccio mainstream14. Una delle conseguenze indirette di quest’impostazione macroeconomica alla distribuzione è che, consolidando i profitti a livello di imprese, quindi di classe capitalistica, questi si annullano e il profitto si rivela essere un mero trasferimento.
1.1.2.4 Causalità dell’investimento sul risparmio: Va sottolineato anche che il circuito di Graziani recepisce l’ipotesi classica che il salario è anticipato (Graziani, 1994). Ciononostante, non c’è l’accumulazione di un “fondo salario”, che nei fisiocratici e negli economisti classici era il grano accumulato nel periodo precedente, bensì una creazione ex novo di potere d’acquisto monetario da parte delle banche che ribalta la causalità fra depositi e prestiti. Quest’inversione di causalità era stata rilevata prima dallo Schumpeter e dal Wicksell, poi dal Keynes del Trattato sulla Moneta che ha introdotto il circuito Keynesiano, seguito in gran parte dagli odierni circuitisti. Se in una società agricola bisognava accumulare prima un risparmio reale (il grano) per poter pagare i salari in anticipo, nella società industriale retta da un’economia monetaria questo non è più necessario. Con la creazione monetaria da parte delle banche, è la spesa che crea il risparmio, aspetto Keynesiano per eccellenza, che è anche il punto di partenza della teoria dei profitti di Kalecki (1942)15. La causalità dei prestiti sui depositi corrisponde logicamente a quella dell’investimento sul risparmio.
1.1.2.5 Scorporo delle banche dal resto del settore produttivo privato: Infine, un altro contributo logico fondamentale del circuito su cui insiste molto Graziani è la divisione del settore privato tra settore bancario che produce moneta, e settore non-bancario che la usa16. Senza separazione fra banche e imprese è difficile integrare la moneta in un modello macroeconomico e questo problema riguarda sia l’analisi neoclassica che quella neokeynesiana (incluso Patinkin). Graziani ricorda infatti che, qualsiasi sia la ragione per cui a fine periodo si detengono delle scorte liquide (pagamento o transazione), il riflusso completo della moneta alla chiusura del circuito nel caso senza crisi (distruzione totale delle liquidità create nel flusso iniziale che finanzia la produzione), corrisponde a una variazione nulla di tali scorte, condizione sulla quale Graziani costruisce un’ipotesi di equilibrio monetario del circuito. Al contrario, la costanza delle scorte liquide rimane un’ipotesi implicita in qualsiasi trattazione macroeconomica classica o neoclassica che, prendendo come periodo di riferimento un lasso di tempo di durata superiore a quello entro il quale la moneta nasce, muore e scompare, fa astrazione della moneta stessa. Ciò equivale a postulare variazioni nulle delle scorte monetarie, trasformando quella che per Graziani è una possibile condizione di equilibrio in un’identità17.
Senza questa suddivisione del settore privato non ci può essere moneta triangolare, cioè moneta nel senso circuitista18, la quale è normativamente una moneta senza “signoraggio” nel senso usualmente dato al termine. Quando esiste, cioè fuori dall’equilibrio a liquidità invariata, questo signoraggio può essere solo “privato”, poiché non c’è né governo, né settore pubblico nel modello canonico di Graziani. Come ha giustamente osservato Riccardo Bellofiore in diverse occasioni, questo è uno dei pochi punti in cui il circuito di Graziani differisce da quello di Parguez.19
1.2 Il modello canonico del circuito monetario di Graziani
Graziani ha presentato diverse varianti del circuito, basate su assunzioni specifiche. Di seguito si presenta il suo modello, che si può definire “canonico”, che è sviluppato nei capitoli IV a VI di Graziani (2003a). Questo comprende un bene, due attività finanziarie e tre settori: quindi ipotizza che lo stesso bene è consumato e investito ed esclude sia il settore pubblico che quello estero20. Nel modello le famiglie possono accumulare risparmio solo in forma liquida o in titoli, passività emesse rispettivamente dalle banche e dalle imprese. Queste brillanti ipotesi semplificatrici sono le condizioni minime per integrare la moneta triangolare in un modello macroeconomico, cosa che non si potrebbe fare se il settore privato non fosse separato fra banche e imprese. Dimostrano che, contrariamente a quanto accade nella teoria monetaria mainstream21, non è necessario introdurre il governo per discutere l’aspetto più pregnante della moneta e della finanza, che riguarda le relazioni fra banche e imprese.
1.2.1 Presentazione del modello
Come discusso, il circuito si focalizza su un singolo periodo che inizia con la fase di flusso durante la quale il polo delle imprese prende a prestito della liquidità monetaria creata dalle banche per un valore equivalente ai salari da distribuire alle famiglie. Le famiglie, che sono il terzo polo del circuito, forniscono in cambio del salario il lavoro occorrente per la produzione di beni di consumo e di beni d’investimento. La moneta creata dalle banche durante il periodo rappresenta dapprima un reddito, per trasformarsi poi in consumo e risparmio quando i beni di consumo prodotti sono venduti alle famiglie. Come nello schema della riproduzione marxiana ripreso anche da Kalecki (1942), il fatto che il monte salari possa essere speso solo per l’acquisto di beni di consumo, implica logicamente che questi ultimi siano acquistati e venduti sul mercato a un prezzo superiore al loro costo di produzione.
Cosa succede all’interno del periodo singolo del circuito? I capitoli V e VI del testo del 2003 sulla Teoria Monetaria della Produzione danno una risposta in 14 equazioni che sono esposte nel riquadro che segue22. Queste forniscono nel loro membro di sinistra il valore di 14 variabili endogene che sono funzione delle stesse endogene e di 9 variabili esogene, che sono considerate prendere valori dati nel periodo esaminato. La maggior parte delle variabili esogene, sono decise dalle imprese e dalle banche. Tra queste, le variabili cruciali del comparto produttivo sono il livello totale dell’impiego N, il tasso reale di investimento b, che sono scelti dalle imprese, e il salario w e la produttività p che, essendo esogeni, presuppongono implicitamente un orizzonte di breve periodo, che intuitivamente si può far coincidere col ciclo annuale della produzione.
Il livello dell’impiego N, è determinato dalle imprese e validato dalle banche quando accordano loro un prestito. Dato il livello del salario w, N determina anche la creazione iniziale di moneta che è quindi endogena. Data la tecnologia di produzione che si assume integrata verticalmente23, attraverso l’impiego N le imprese e le banche fissano anche la produzione reale X, e, nel momento che decidono la quota del prodotto destinata all’investimento reale b e la fanno validare dalle banche, fissano anche la proporzione di lavoratori che allocano alla produzione di beni di consumo e di beni di investimento. Nel circuito le decisioni delle famiglie sono quindi subordinate a quelle delle imprese e delle banche, poiché le prime decidono sia il livello della produzione (via N) 24, che quello della distribuzione (via b), e attraverso quest’ultimo il livello dei prezzi (p).
Come si vede dalla prima relazione nella Figura 1, la ripartizione del prodotto fra consumo e investimenti (o del lavoro, visto che anche la produttività è data), determina il livello dei prezzi, che risulta uguale al prodotto di un margine di profitto, dato dal rapporto tra la propensione al consumo e uno meno la propensione all’investimento reale, moltiplicato per un termine di costo unitario, dato dalla somma del costo del lavoro e del costo dell’interesse per unità di prodotto. Questa relazione di prezzo è centrale perché determina la distribuzione dei redditi che, come osserva Graziani, il circuito riprende da Kalecki (1942). Implica che i prezzi non dipendono dalla quantità di moneta, contrariamente al punto di vista monetarista25.
Figura 1:Blocco macro-monetario e finanziario nel modello canonico del circuito di Graziani

È opportuno soffermarsi sul significato del margine di profitto nella dinamica temporale che intercorre fra finanza iniziale e finanza finale nel circuito di Graziani, che, va ricordato, si fonda sulla sua lettura del finance motive di Keynes (Graziani, 1984c e 1987)26. Mario Seccareccia (2004) ha sottolineato le origini wickselliane del circuito di Graziani in un suo notevole contributo a un volume in onore di Graziani che contiene anche diverse altre analisi circuitiste di grande interesse. Le idee di Wicksell, per cui si rimanda anche a Bellofiore (1998), hanno influenzato “equilibristi generali” come Hayek e Lindbeck, ma anche il Keynes del Trattato sulla Moneta che, come dimostra Seccareccia e come ha sostenuto anche Graziani (1981), è sostanzialmente coerente col Keynes della Teoria Generale. Seccareccia ha inoltre sollevato a diverse riprese un’interessante obiezione sul markup fisso che appare nella relazione di prezzo (1) che Graziani deriva dall’uguaglianza fra domanda e offerta globale. Secondo lui, in un modello propriamente post-keynesiano, il markup dovrebbe essere variabile e non fisso (Eichner, 1973) e, soprattutto, non dovrebbe derivare da un’eguaglianza “walrasiana” fra domanda e offerta globale. Se quest’obiezione ha molti meriti, non inficia però il fatto già rilevato che nel circuito, come nell’analisi di Sraffa, sono le imprese a decidere e non i consumatori. Infatti, una volta concordato il valore monetario iniziale della produzione con le banche, le imprese fissano e concordano implicitamente con le banche anche le altre variabili della produzione e della distribuzione ad eccezione del risparmio delle famiglie e della frazione di quest’ultimo detenuta sotto forma liquida. È peraltro solo il risparmio liquido delle famiglie che rappresenta per loro un problema, perché genera un uguale indebitamento addizionale nei confronti del settore bancario, che è a sua volta per loro una perdita di reddito reale perché sono costrette a prelevare il pagamento degli interessi sui propri profitti27. Le imprese sono invece indifferenti al risparmio delle famiglie sotto forma di titoli, poiché, dato che controllano sia i prezzi che la distribuzione, possono ripercuotere su queste l’intero costo degli interessi sui titoli, fissando i prezzi in modo da ottenere il tasso di interesse sulle obbligazioni necessario per compensare quello che le banche offrono sui depositi.
Questo sottolinea un aspetto essenziale del circuito che è che all’interno del periodo di produzione, che è anche quello della creazione-distruzione totale di moneta nel caso senza crisi, avviene una redistribuzione del valore-salario iniziale della produzione finanziato dalla moneta credito (finanza iniziale) fra quella che poi diventa al momento della finanza finale la sua ripartizione fra salari, profitti e interessi28.
Inoltre, se è vero che nel periodo compreso fra la finanza iniziale e la finanza finale le imprese determinano un markup che è effettivamente fisso, dato che questo periodo è di durata arbitraria, si può fare tendere a zero, permettendo al limite un aggiustamento continuo del markup e quindi, in sostanza, una sua variabilità temporale. Al di là di quest’aspetto meramente formale, il punto di sostanza resta che nel modello di Graziani sono le imprese a fissare sia il livello che la composizione del prodotto e dell’occupazione e, dato che quest’ultima fissa il markup, hanno in mano tutte le leve della decisione. Il fatto che il livello del markup si deduca eguagliando domanda e offerta globale, anche se compatibile con Hayek o Walras, è soprattutto un’applicazione del concetto di domanda effettiva di Keynes29. Di fatto, generalizzando su basi Kaleckiane l’ipotesi di mercati competitivi accolta da Keynes, nel modello di Graziani le imprese possono fissare i prezzi su basi oligopolistiche e disporre in pratica della stessa capacità di determinare prezzi e quantità di quella che avrebbero in caso di monopolio puro.
Come sottolinea Graziani (2003a, pp. 103-104) è chiaro dalle relazioni (7)-(9) sui profitti, che: (i) il tasso di profitto può, come in Kalecki, essere positivo solo quando le imprese investono più di quanto le famiglie non risparmino (b>s); (ii) i profitti monetari dipendono direttamente dal livello dei prezzi e aumentano con il tasso di interesse che le imprese pagano alle famiglie sui titoli iB, che è a sua volta funzione di iL e iD; e iii) i profitti reali non dipendono dal tasso di interesse iB che le imprese pagano sui titoli che vendono alle famiglie, ma, attraverso l’aumento dei prezzi, si riducono in funzione del tasso di interesse pagato alle banche iL che è un trasferimento di reddito reale quando sia esaurita ogni possibilità di aumentare iB. Quando la propensione all’investimento e la propensione al risparmio coincidono (b=s), i (sovra-)profitti si annullano e ci si trova nel caso della concorrenza perfetta. Nel caso di risparmio delle famiglie nullo (s=0), “i capitalisti guadagnano quello che spendono mentre i lavoratori spendono ciò che guadagnano”30.
Le relazioni (10) – (14) illustrano la formazione dei tassi di interesse in base all’eguaglianza fra domanda e offerta di risparmio al momento di chiusura del circuito. La relazione (10)31 traduce quest’eguaglianza sotto un’ipotesi ragionevole sulla specificazione dell’offerta e della domanda di titoli32 e, una volta verificata, consente alla (12) di determinare sia la domanda che l’offerta di risparmio. La (10) implica che, perché si abbia eguaglianza fra offerta e domanda di risparmio, una volta fissato il tasso di interesse iD pagato dalle banche sulle scorte liquide, il tasso di interesse iB sui titoli emessi dalle imprese si determina come funzione lineare di iL quando a e b sono dati, livello che non corrisponderà necessariamente alla piena occupazione (vedasi §1.3). Se, oltre a questo, si ammette che tutto il risparmio delle famiglie è investito in titoli emessi dalle imprese (bd=1), si ha anche una variazione nulla delle scorte liquide che può essere considerata in prima approssimazione una condizione per l’equilibrio finanziario delle imprese (Graziani, 2003a, p. 125)33.
Le 14 variabili endogene: bd, B, C, iB, Im, Ir, DL, p, P, Pr, r, S, X, Y, sono determinate dalle relazioni (1)-(14) e dalle variabili esogene, come riassunto nel riquadro che segue. Le esogene34 comprendono due variabili macroeconomiche “strutturali”: la produttività p e il salario w. Oltre a queste, ci sono sette variabili di decisione, delle quali due sono determinate dalle famiglie: il tasso di risparmio s e la preferenza per la liquidità b. Le altre sono determinate dalle imprese: l’impiego totale N, la propensione reale all’investimento b e il coefficiente di preferenza per il credito delle imprese m; o dalle banche: il tasso di interesse pagato dalle imprese sui prestiti iL e il tasso di interesse pagato dalle banche sui depositi iD.
Figura 2: Lista delle variabili esogene e endogene del modello

1.2.2 Alcune simulazioni numeriche
Per illustrare il comportamento del modello di Graziani in un singolo periodo, si presentano alcune simulazioni di statica comparata ottenute dando dei valori virtuali alle variabili e ai parametri esogeni che determinano una soluzione centrale (o “di controllo”) per le variabili endogene che viene poi confrontata con quella ottenuta modificando una sola delle esogene alla volta. Questa seconda soluzione corrisponde a una “derivata parziale” del sistema rispetto a un cambiamento di una sola delle esogene in prossimità della soluzione centrale. Tale sensibilità illustra la meccanica del modello (che è diversa da quella del modello neoclassico). Non pretende fornire una descrizione realistica di cosa accadrebbe se nella realtà la variabile esogena si modificasse come indicato. Lo scopo non è infatti l’uso del modello per la formulazione di proiezioni o scenari, ma la comprensione delle sue proprietà. In simulazioni più realistiche altre esogene si muoverebbero insieme all’esogena considerata e quindi eventuali scenari alternativi dovrebbero calcolare l’effetto del cambiamento di varie esogene contemporaneamente (si veda l’esempio del § 2.4).
1.2.2.1 Simulazione di riferimento: Se si danno i valori seguenti alle variabili e ai parametri esogeni si ottengono i valori riportati nel riquadro di destra per le variabili endogene35:
Figura 3: Valore delle esogene e delle endogene nella soluzione di riferimento
1.2.2.2 Variazione esogena di N: Partendo da questa soluzione di riferimento, se si fa variare l’occupazione totale da 700 a 1400 si può vedere nelle tre simulazioni descritte nel grafico 1 che le variabili distributive (S, P, Im, B, L) aumentano proporzionalmente mentre i principali parametri finanziari (bd, iB, r) e in particolare il tasso di profitto restano immutati. Il grafico non è riprodotto, ma anche i prezzi restano immutati, mentre, nella logica Keynesiana del circuito sia il consumo che il reddito reale delle famiglie aumentano per effetto dell’aumento dell’attività.
Grafico 1: Sensibilità a una variazione del livello di occupazione N deciso dalle imprese [700-1400]

1.2.2.3 Variazione esogena di b: La simulazione successiva è relativa a una variazione del tasso di investimento reale b fra 0.2 e 0.5 e illustra che gli effetti di questa variazione passano principalmente attraverso il tasso di profitto reale e i prezzi, che aumentano fortemente.
Controllando i prezzi, le imprese, che privilegiano l’autofinanziamento, li aumentano e così aumentano sia i profitti nominali che l’investimento in valore monetario. Al contrario sia il consumo reale che il reddito reale delle famiglie si contraggono a causa dell’aumento dei prezzi, poiché in questa variante non ci sono né aumenti salariali, né l’aumento della produttività che in uno scenario realistico sarebbero contestuali a un aumento degli investimenti. Questo conferma però che la meccanica del modello consente alle imprese di finanziare un aumento degli investimenti attraverso una diminuzione del reddito e del consumo reale delle famiglie.
Grafico 2: Sensibilità a una variazione del tasso di investimento b [0.2-0.5]

Dal punto di vista della politica economica non basta quindi creare le condizioni per aumentare i profitti e gli investimenti, ma bisogna anche aumentare i salari e la produttività perché aumenti il benessere collettivo. In conclusione, attraverso b si modifica il livello dei prezzi, il tasso di investimento, il tasso di profitto e quindi il tasso di autofinanziamento che passa dal 29% all’82%.
1.2.2.4 Variazione esogena di s: Facendo variare il tasso di risparmio delle famiglie s tra il 5% e il 25% si osserva che risparmio, titoli detenuti e liquidità aumentano, mentre i profitti nominali e reali diminuiscono per la caduta dei prezzi e perché il tasso di investimento resta costante, mentre gli investimenti nominali diminuiscono per effetto della caduta dei prezzi. Alla fine, mentre il consumo nominale e quello reale restano costanti, il reddito reale aumenta per effetto della riduzione dei prezzi e dell’aumento del risparmio che gonfia la ricchezza detenuta in titoli e, dato il contestuale aumento della liquidità, determina un maggiore indebitamento delle imprese presso le banche.
Grafico 3: Sensibilità a una variazione del tasso di risparmio s [5%-25%]

1.2.2.5 Variazione esogena di p: Variando la produttività p tra 1.1 e 1.5 l’effetto meccanico si ha sui prezzi, che diminuiscono facendo aumentare il consumo e il reddito reale.
Grafico 4: Sensibilità a una variazione del tasso di produttività p [1.1-1.5]

Viceversa, le variabili nominali e monetarie restano costanti.
1.2.2.6 Variazione esogena di w: Facendo variare il salario nominale w tra 8 e 12 il primo effetto si fa sentire sui prezzi, che aumentano fortemente.
Grafico 5: Sensibilità a una variazione del salario w [8-12]

Tutte le variabili nominali di conseguenza crescono, mentre i parametri finanziari restano costanti, come anche il consumo e il reddito reale delle famiglie per i quali i grafici non sono riprodotti.
1.2.2.7 Variazione esogena di m: Una variazione del coefficiente di preferenza delle imprese per il credito bancario fra 0.2 e 0.6 aumenta i prestiti presi dalle banche e riduce la raccolta di risparmio (B).
Grafico 6: Sensibilità alla variazione del coeff. di preferenza delle imprese per il credito bancario m [13%-33%]

Dato che i tassi di interesse sui prestiti si presumono costanti, l’aumento dell’indebitamento non riduce i profitti nominali né gli investimenti se non marginalmente. Anche il tasso di profitto resta costante, il tasso di interesse sulle obbligazioni scende leggermente mentre la quota di risparmio che le famiglie detengono sotto forma di titoli si riduce. La riduzione del tasso di interesse sul debito delle imprese verso le famiglie provoca una leggera riduzione dei prezzi, che provoca una riduzione delle variabili nominali (consumo, investimento e risparmi) che è impercettibile graficamente, ma in termini reali sia il consumo che il reddito restano costanti (grafico non riprodotto).
1.2.2.8 Variazione esogena di b: La figura 7 esamina l’effetto di una variazione del coefficiente di liquidità delle famiglie b da 150 a 500.
Grafico 7: Sensibilità a una variazione del coefficiente di liquidità delle famiglie β [0.01-0.2]

Anche qui si lasciano costanti sia il tasso di interesse sui depositi iD e quello sui prestiti iL. Il tasso di interesse consentito dalle imprese sui loro titoli iB aumenta leggermente, e diminuisce la domanda di titoli, mentre non muta il tasso di profitto. I prezzi rimangono costanti, così come i profitti nominali, il risparmio e gli investimenti, mentre, come osservato, il risparmio delle famiglie investito in titoli diminuisce a causa dei maggiori prestiti che le imprese sono costrette a richiedere alle banche per via dell’aumentata preferenza per la liquidità delle famiglie. Il consumo e il reddito reale non mutano, né cambiano i loro livelli nominali.
1.2.2.9 Variazione esogena di iL: Si considera l’aumento del tasso di interesse sui prestiti alle imprese iL dal due al nove percento. Si vede sul Grafico 8 che, data la costanza dei parametri monetari esogeni (propensioni alla liquidità delle imprese e delle famiglie e tasso sui depositi), il principale effetto di un aumento di un tasso di interesse sui prestiti alle imprese è quello di aumentare l’offerta di titoli da parte delle imprese che richiede un aumento del tasso di interesse pagato sui loro titoli.
Così facendo, le imprese compensano la riduzione dell’indebitamento verso le banche (DL), che è provocata dal maggior costo dell’interesse, con l’aumento del loro debito verso le famiglie. Al tempo stesso, tramite l’equazione dei prezzi, le imprese neutralizzano gli effetti reali dell’aumento della spesa per interessi cosicché non cambiano sostanzialmente né il risparmio delle famiglie, né i profitti, né gli investimenti monetari. Non ci sono quindi neanche effetti reali sul consumo e sul reddito delle famiglie. Tuttavia, a causa della maggiore spesa per interessi, il totale del loro debito obbligazionario aumenta rapidamente in proporzione dell’investimento effettuato (dal 10% al 41% dell’investimento).
Grafico 8: Sensibilità a una variazione del tasso di interessi sui prestiti delle banche alle imprese iL [1.0-1.05]

1.2.2.10 Variazione esogena di iD: Infine si considera un aumento del tasso di interesse pagato dalle banche sui depositi delle famiglie da 0,1% a 0,7%.
Grafico 9: Sensibilità alla variazione del tasso di interessi sui prestiti delle banche alle imprese iD [0,1%-0,7%]
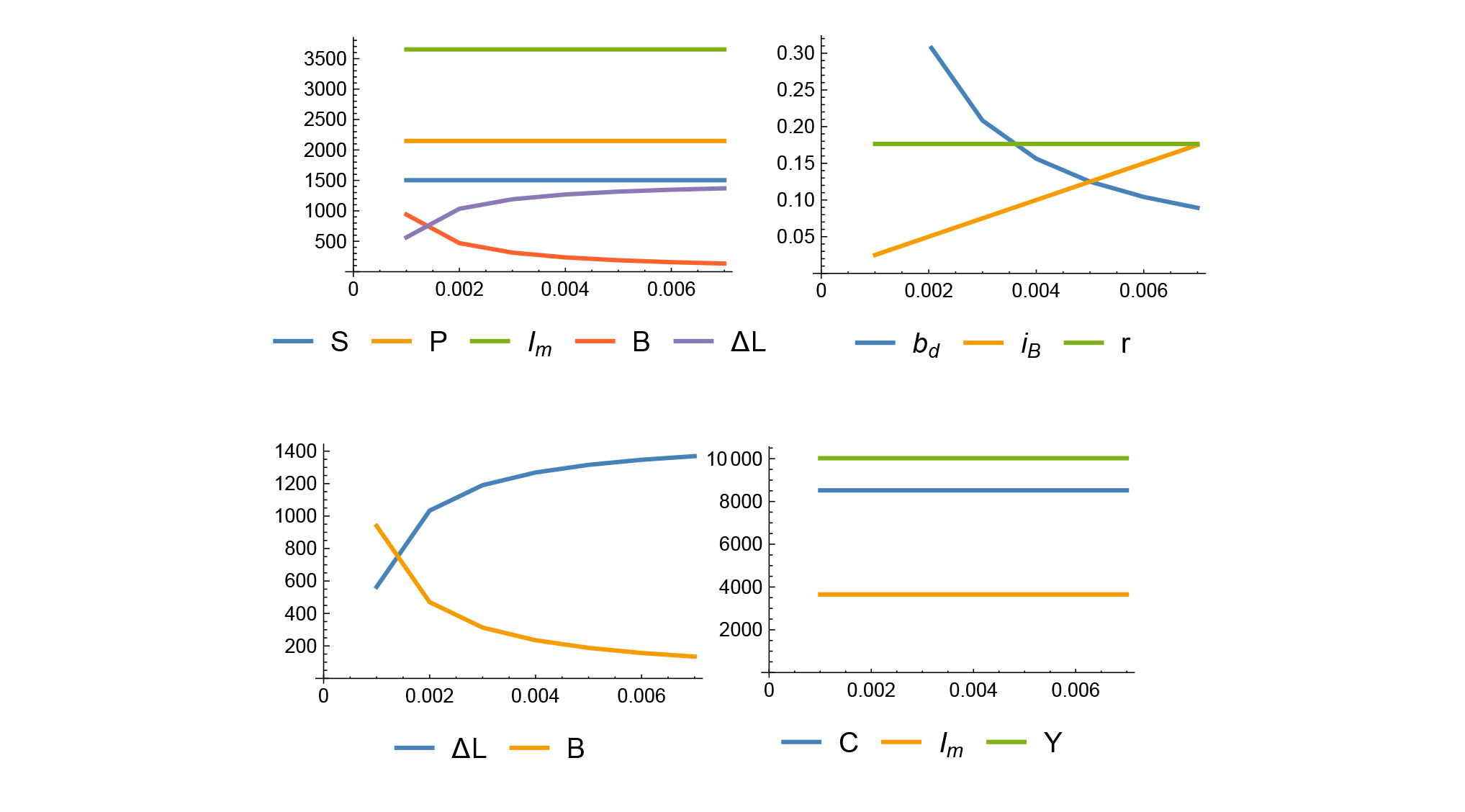
Questo provoca una riduzione della domanda di titoli e obbliga le imprese ad aumentare il tasso di interesse offerto sui titoli, che però non riesce a impedire un aumento della liquidità delle famiglie e quindi del loro indebitamento verso le banche. Il totale del loro debito obbligazionario aumenta quindi rapidamente in proporzione dell’investimento effettuato (dal 15% al 37% dell’investimento). Né le variabili nominali (risparmi, profitti, investimenti, reddito e consumo) né i prezzi variano e quindi restano immutati anche i consumi e il reddito reali.
1.3 La chiusura del circuito e la doppia condizione di equilibrio reale e finanziario
Al termine del capitolo VI, Graziani (2003a) osserva che nel circuito ci sono due condizioni di equilibrio che determinano il livello di disoccupazione e che investono le variabili monetarie del modello e i tassi di interesse. Per vederlo, si può partire dalla relazione (10) che fissa il tasso di interesse sui titoli emessi dalle imprese iB e che assieme alla (12) determina la proporzione bd del risparmio investita in titoli, date le preferenze per la liquidità dei consumatori (b), quelle per il credito delle imprese (m) e i tassi di interesse sui depositi iD e sui prestiti alle imprese iL. La (10) esprime l’equilibrio della domanda e dell’offerta sul mercato dei titoli come una relazione lineare fra il tasso di interesse che le imprese offrono ai risparmiatori sui titoli e il tasso sui prestiti che le banche consentono alle imprese. La figura 436 illustra questa relazione nel piano cartesiano di ascissa iL e di ordinata iB. La retta di inclinazione b1 (linea blu) corrisponde all’equilibrio iniziale del mercato dei capitali. Ponendo la condizione aggiuntiva bd=1, si può calcolare il valore della coppia (iB,iL) tale per cui tutto il risparmio delle famiglie sarà investito in titoli, ciò che avviene al punto C, di cui si può supporre inoltre che rifletta inizialmente condizioni di piena occupazione. Il punto C rispetta la costanza delle scorte liquide detenute dalle famiglie, e quindi una quantità invariata di moneta, ipotesi che, come osserva Graziani, sono anche quelle accolte da Keynes nella Teoria Generale e che implicano quindi un indebitamento invariato delle imprese verso le banche. Quest’ultimo può essere interpretato come una condizione per l’equilibrio finanziario dinamico delle imprese.
Figura 4: Dinamica della variazione della preferenza per la liquidità

Nella figura 4, questo felice connubio si realizza quando, dati gli altri parametri accolti nella simulazione di controllo, le banche fissano il tasso di interesse iL sui prestiti all’8% e le imprese fissano il tasso sulle loro obbligazioni al 4%. Come indicato, il valore particolare scelto per la coppia (iB, iL) al punto C corrisponde per ipotesi alla piena occupazione e alla costanza delle scorte liquide delle famiglie, una situazione che logicamente dovrebbe portare le imprese a mantenere la piena occupazione nel periodo successivo. Se però durante il periodo di produzione il coefficiente di preferenza per la liquidità aumenta da b1 a b2, la retta che rappresenta gli equilibri del mercato dei capitali ruota verso l’alto (linea arancio). In tal caso, se le banche lasciano invariato il loro tasso sui prestiti iL all’8%, il nuovo tasso sui titoli si assesterà al 5% (punto C’), livello che non è sufficiente alle imprese per raccogliere l’intero risparmio. È quindi plausibile che all’inizio del periodo successivo le imprese, che hanno visto il loro indebitamento aumentare in proporzione all’investimento, siano portate a ridurre la produzione e l’occupazione per aver subito un trasferimento reale di reddito verso le banche. Infatti, a causa dell’aumentata preferenza per la liquidità, il risparmio delle famiglie investito in titoli si riduce e, affinché le scorte liquide restino immutate, sarebbe necessario che le banche fissassero il tasso di interesse sui prestiti iL al 10%, ciò che porterebbe le imprese a offrire un tasso iB del 6,25% sui loro titoli (punto D).
Il circuito mostra quindi che ci sono due condizioni di piena occupazione delle quali l’economia keynesiana tradizionale considera solo la prima: i) il tasso di interesse e il livello dell’investimento devono permettere la piena occupazione, come usualmente richiedono i modelli Keynesiani; ii) ci dev’essere un equilibrio finanziario fra banche e imprese la cui mancata realizzazione può essere causa di disoccupazione, fatto che non può essere esplicitato se non si scinde in due il settore privato isolando le banche (Graziani, 2003a p. 128)37. Questo spiega perché la piena occupazione è estremamente instabile dal punto di vista della successione dinamica dei singoli periodi. La dinamica prefigurata da Graziani è, come in Kalecki (1954), quella di una successione di squilibri di breve periodo. Prevale quindi il caso “malthusiano” di chiusura del circuito “con crisi”.
2. Cenni sulla pertinenza empirica del circuito
In questa sezione si riportano i risultati di lavori svolti in passato finora non pubblicati e si presentano dati più recenti sull’evoluzione di alcuni aggregati macro-finanziari relativi a verifiche empiriche del circuito. Si presenta anche una simulazione del modello di Graziani atta a darne una possibile spiegazione.
Nel 2008 l’Istituto Bei finanziò uno studio svolto presso l’università di Nizza nel quale la teoria del circuito monetario fu sottoposta a test empirici fatti sui paesi di Visegrad (Repubblica Ceca, Repubblica Slovacca, Slovenia e Ungheria) e la Turchia con gli strumenti econometrici in voga all’epoca.
Figura 5: Sintesi dello studio Starebei del 2008

La ricerca confermò la validità del circuito monetario. Cinque ipotesi furono sottoposte a stima econometrica per i paesi Visegrad e i risultati sono riassunti nella Figura 5. Su base di quest’esperienza si può dire che una delle difficoltà dei test empirici sul circuito monetario è che non si osserva la finanza iniziale (si veda anche la sezione 2.3). Sotto certi aspetti si potrebbe dire che la finanza iniziale è la somma dei salari, sotto altri aspetti si può dire che è il PIL, cioè (circa) la somma dei redditi da lavoro e da capitale, anche se entrambi gli aggregati in contabilità nazionale sono osservati a chiusura dell’esercizio e sono quindi indicatori della finanza finale a prezzi di mercato. In realtà non c’è una variabile ovvia tra quelle osservabili che corrisponde esattamente al concetto di finanza iniziale. Occorrerebbe quindi esaminare gli indicatori al costo di produzione e integrare meglio nelle stime quello che si chiama il processo generatore dei dati (Hendry & Richard [1983] 1993).
2.2 La creazione monetaria e la dinamica dei salari e della ricchezza finanziaria38
Per definizione, non essendo neutra rispetto alla formazione del valore, la moneta circuitista può incidere sui prezzi relativi. In particolare, il finanziamento monetario della speculazione può favorire la crescita più rapida del valore di mercato delle attività finanziarie relative al circuito del risparmio accumulato (circolazione finanziaria o circuito del capitale), piuttosto che quello delle attività legate alla generazione dei redditi correnti, e in particolare i salari (circolazione industriale o circuito del reddito).
Infatti, una volta accettata la definizione di moneta come passività “terza” emessa dalle banche per effettuare i pagamenti (Schneider, 1962), si capisce anche che la liquidità creata dal credito e distrutta al momento del suo rimborso può essere prestata nel frattempo per finanziare l’acquisto di attività reali e titoli finanziari e quindi influenzare il loro prezzo. Inoltre, esulando dal quadro semplificato del modello canonico del circuito, all’interno del periodo di produzione, la moneta può anche essere creata dalle banche per l’acquisto di titoli, e quindi potenzialmente svolgere un ruolo speculativo39. Con un piccolo salto logico che andrebbe esplicitato, il circuito può così illustrare e spiegare la finanziarizzazione, che, pur essendo un concetto discutibile che andrebbe precisato (Toporowski & Mitchell, 2013&14), resta uno dei fenomeni macro-finanziari più macroscopici degli ultimi decenni.
I grafici che seguono illustrano le evoluzioni divergenti dei prezzi relativi delle attività finanziarie e dei flussi legati alla creazione del reddito, cioè la cosiddetta inflazione del prezzo degli attivi (Toporowski, 2000), e possono essere interpretati in chiave circuitista.
Grafico 10: Salari, interesse e attivi finanziari USA 1954-2016

Se prendiamo ad esempio il caso degli Stati Uniti nel Grafico 10, comparando l’evoluzione a lungo termine di un paniere di beni salariali e di un paniere di beni finanziari si osserva che l’indice salariale ha perso terreno permanentemente rispetto a quello finanziario. Se un lavoratore avesse avuto 3 $ nel 195740 e li avesse investiti in un indice che fosse progredito allo stesso ritmo del valore dei salari nell’industria manifatturiera americana (linea marrone), nel 2016 avrebbe avuto 32 $. Se invece l’avesse investito in un indice che si fosse comportato come quello delle obbligazioni a lungo termine americane, nel 2016 avrebbe accumulato un capitale di 100 $ (linea blu). La cesura fra le curve blu e marrone avviene nel 1979-1980, anni a partire dai quali divergono, come confermato dall’evoluzione della linea verde, che illustra la differenza accumulata fra le due prime e che diventa positiva a partire dal 1982. Le colonne in giallo in basso nel grafico rappresentano invece l’evoluzione del rapporto tra attività finanziarie e PIL negli Stati Uniti, che è passato da un valore inferiore a due fino agli anni Ottanta a un valore di circa cinque nel 2016. La finanziarizzazione si manifesta quindi nella forma di un aumento del valore degli stock finanziari rispetto a quello dei flussi produttivi che riflette un’evoluzione negativa del prezzo relativo del lavoro. Lo stesso tipo di evoluzione si può osservare nel grafico che segue per il Regno Unito, per dei periodi che non coincidono appieno con quelli degli Stati Uniti, ma che sono compatibili con un’interpretazione analoga.
Se nel grafico 11 si prende un indice pari a una sterlina nel 1963 e questo avesse progredito come i salari orari nel settore manifatturiero inglese (linea marrone), nel 2016 questo avrebbe raggiunto un valore nominale di 46 UKP.
Grafico 11: Salari, interesse e attivi finanziari UK 1960-2016

La stessa sterlina del 1963, investita invece in un indice che fosse aumentato come il tasso a lungo termine sulle obbligazioni di Stato inglesi (linea blu nel grafico), sarebbe arrivata a valere 54 UKP nel 2016. La divergenza accumulata fra i due indici (linea verde) è rimasta negativa (cioè favorevole ai salari) tra il 1970 e il 1996 e ha toccato il suo minimo nel 1982, anno a partire dal quale ha cominciato a recuperare per diventare positiva nel 1996 e raggiungere il valore di circa 16 nel 2016. Per il periodo in cui i dati sono disponibili, che comincia nel 1979, il rapporto tra attività finanziarie e PIL, che era di 1,85 nel 1979, è aumentato a 3,6 nel 1991, per salire a 15,1 nel 2008 ed è poi sceso a 11,7 nel 2016.
Grafico 12: Salari, interesse e attivi finanziari EZ 1973-2016

Anche per quanto riguarda la zona Euro, i dati del grafico 12 indicano che un euro del 1973, investito in un indice che fosse cresciuto come i salari orari nel settore manifatturiero (linea marrone), nel 2016 avrebbe raggiunto il valore nominale di 11 Euro. Lo stesso euro, investito in obbligazioni a lungo termine, avrebbe raggiunto un valore nominale di 20 Euro nel 2016 (linea blu). La divergenza accumulata fra i due indici (linea verde) è rimasta in territorio negativo dal 1973 al 1986 per poi eccedere 10% nel 1989 e raggiungere 48% nel 2016. Il rapporto tra attività finanziarie e PIL che era di 4,83 nel 1999, è salito a 6,88 nel 2016.
L’evoluzione sfavorevole del prezzo relativo del lavoro rispetto a quello di attività finanziarie come le obbligazioni a lungo termine documentata nei grafici precedenti è confermata quando si esaminano altre forme di destinazione del risparmio come fatto nel grafico 13 qui di seguito che esamina l’evoluzione dei prezzi relativi di varie attività finanziarie e reali confrontando il loro valore nominale nel 2015 a quello del 1995 per il Regno Unito41. Si vede sul grafico che il valore del totale delle attività finanziarie è stato moltiplicato per 5,4, mentre quello dell’indice dei prezzi residenziali è stato moltiplicato per 3,5, quello degli attivi fissi (investimento reale) per 2,6, quello delle obbligazioni a lungo termine per 2,3 e quello delle azioni per 2,0. A confronto, l’indice basato sul PIL nominale assume nel 2015 un valore che è 2,2 volte quello del 1995 e per quello dei salari orari questo rapporto è 1,9. Si vede quindi che la crescita del valore delle attività finanziarie è stata molto più veloce di quella del valore dei flussi legati alla produzione corrente.
Grafico 13: Confronto fra diversi indici finanziari 1995-2015

In particolare, le attività finanziarie sono cresciute più velocemente del PIL al punto che il loro valore si è più che duplicato rispetto al PIL (2,2). Per gli attivi fissi, indicativi dell’evoluzione del valore dell’investimento “reale”, questo rapporto è invece di 1,2. Nello stesso periodo i salari nominali sono invece cresciuti meno rapidamente del PIL per cui hanno perso ancor più di quest’ultimo rispetto alle attività finanziarie.
Questi grafici documentano come nel corso degli ultimi decenni vi sia stato un movimento parallelo di aumento del peso delle attività finanziarie rispetto al PIL, cioè della rendita finanziaria, accompagnato da un’evoluzione della distribuzione dei redditi sfavorevole al lavoro. Non è questa la sede per entrare nel dettaglio di queste evoluzioni, ma la sostanza è abbastanza intuitiva: se si ammette che le banche o il sistema finanziario nel suo complesso possono creare liquidità (e/o quasi-liquidità) prendendo posizioni speculative senza veri e propri limiti, è logico che questa liquidità si orienti verso le attività a rendimento più elevato. Se inoltre il sistema permette un afflusso costante di nuova liquidità verso i mercati finanziari (Toporowski, 2000, pp. 31-41), si possono creare le condizioni per cui le aspettative di guadagni in conto capitale sempre crescenti si auto-alimentano e eccedono qualsiasi rendimento offerto dall’accumulazione reale.
2.3 Uno sguardo agli aggregati macro-finanziari più recenti
Per completare il quadro empirico, in questa sezione si esaminano i dati relativi agli anni più recenti. Come argomentato in precedenza, la difficoltà per la valutazione empirica del circuito è che non si osserva la finanza iniziale42. Si osservano invece vari aspetti della finanza finale, in particolare i debiti e le liquidità accumulati a fine periodo, nonché il risparmio. Dal punto di vista conoscitivo, il punto interessante è ovviamente quello della causalità dei prestiti sui depositi. Come già detto, in quest’ottica si deve considerare che l’acquisto di un titolo da parte delle banche ha lo stesso effetto che un prestito, cioè crea moneta, senza però creare necessariamente un reddito, e questo può contribuire a spiegare le manifestazioni del processo di finanziarizzazione43. Le banche, e più in generale il sistema finanziario, acquistando e vendendo titoli all’interno del circuito del risparmio, possono quindi aumentare il loro prezzo determinando un aumento del valore dei beni accumulati nel passato rispetto ai valori della produzione corrente (nella circolazione industriale).
Alcuni grafici estesi al periodo più recente permettono una rapida verifica indiretta di questa e di altre delle principali idee del circuito. Nel grafico 14 si osservano a sinistra il PIL e il valore dei prestiti all’attivo degli intermediari finanziari e monetari della zona euro. Si nota una certa corrispondenza. Nel grafico a destra si riportano invece le stesse variabili in variazione e anche qui c’è una certa corrispondenza, anche se non è perfetta.
Grafico 14: Area Euro – Prestiti e GDP nominale: livello (sinistra) e variazione(destra) 1990Q1-2021Q1

Il grafico 15 di sinistra riguarda le passività emesse dalle imprese sia sotto forma di prestiti che di titoli e li confronta al monte salari aggregato negli ultimi 15 anni44. Sono evidenziati due sottoperiodi nei quali la riduzione dei prestiti accesi dalle imprese ha determinato una decelerazione dei salari.
Grafico 15: Area Euro – Indebitamento imprese (sin.) e prestiti delle banche (destra) 1990Q1-2021Q1

Nel grafico 15 di destra, che presenta in stock e in variazione le due componenti dei prestiti e dell’acquisto di titoli all’attivo delle banche della zona Euro, si vede che l’evoluzione dei titoli detenuti e dei prestiti è stata abbastanza correlata, che sia in livelli o in variazioni.
Grafico 16: Area Euro – Indebitamento delle imprese: rapporto tra flussi e consistenze: 1990Q1-2021Q1

Un fatto notevole è che il rapporto fra flussi e stock nel corso del tempo è andato riducendosi, come si vede nel grafico 16 qui accanto, che descrive l’evoluzione del debito al passivo delle imprese: i prestiti (F4) in blu e i titoli (F3) in arancione, entrambi espressi in percentuale dei valori dei rispettivi stocks. Si può innanzitutto osservare che questa percentuale è bassa: il valore della moneta presa a prestito durante l’anno è stato dell’ordine del due percento rispetto al valore dei debiti e dei prestiti accumulati, ed è sceso all’un percento negli anni successivi al 2009. Si osserva dunque nel corso del tempo una riduzione del valore dei flussi rispetto agli stocks, che è compatibile con una spiegazione dell’aumento del prezzo relativo degli attivi finanziari che rappresentano la ricchezza già accumulata rispetto ai flussi come il salario.
Grafico 17: Area Euro – Depositi delle e delle imprese in % del PIL: 1990Q1-2021Q1

Questo ultimo aspetto è confermato nel grafico 17 a sinistra che mostra come il rapporto tra depositi e PIL per le famiglie e le imprese dell’area Euro è aumentato quasi costantemente negli ultimi 25 anni, di circa uno per cento del PIL per le famiglie e di 0,5 punti percentuali del PIL per le imprese. A conferma indiretta della pertinenza del circuito, l’ipotesi di nullità delle variazioni delle scorte liquide non è quindi verificata empiricamente (cf. §1.1.2.2 e §1.1.2.5).
2.4 Il modello canonico del circuito e la finanziarizzazione
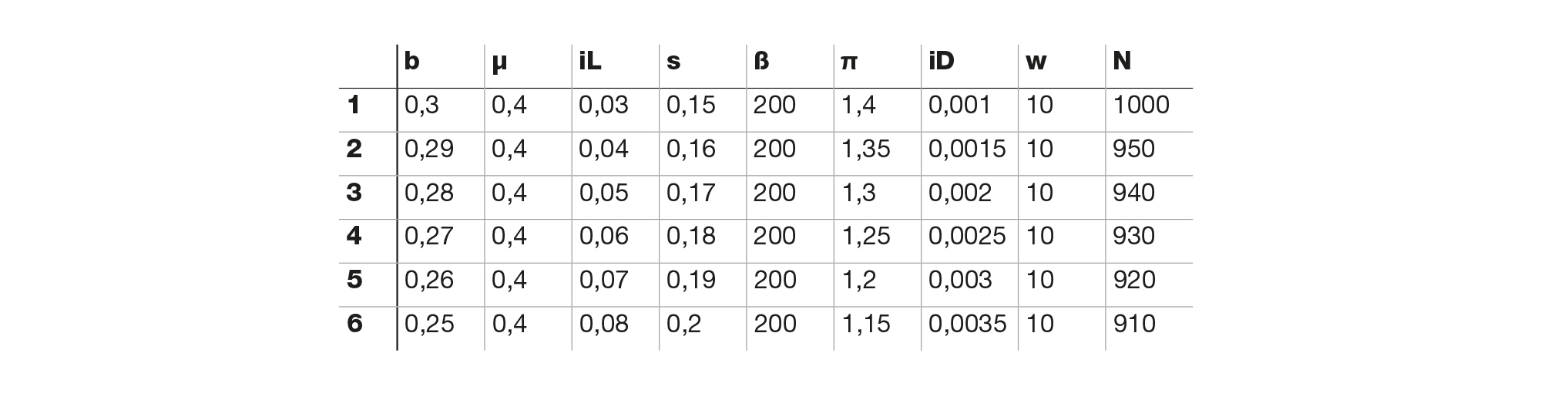
Il circuito di Graziani descrive un’economia monetaria della produzione che include gli aspetti essenziali della finanza e in particolare l’accumulazione di moneta e di capitale, ma che resta pur sempre un modello di flusso. Per affrontare bene il tema della finanziarizzazione, bisognerebbe aggiungere al “blocco” della Figura 1 delle relazioni relative al comportamento degli stocks accumulati e del loro prezzo a partire della chiusura del primo periodo del circuito. Ciononostante, anche senza queste modifiche, il modello può riprodurre vari aspetti della finanziarizzazione in un esercizio di statica comparata, restando cioè nel contesto di un equilibrio di singolo periodo che si ripete in maniera recursiva. Questo risultato si può ottenere costruendo uno scenario per le variabili endogene del modello, che combina alcuni dei cambiamenti sulle esogene esaminati individualmente al §1.2.2. Lo scenario simula l’aumento della rendita finanziaria con l’aumento dei tassi di interessi esogeni iD e iL, che hanno per effetto di aumentare anche il tasso di interesse endogeno sulle obbligazioni iB45. In questo contesto è lecito ipotizzare un aumento parallelo del tasso di risparmio s. Alla luce dell’argomentazione del § 1.3, l’aumento della rendita finanziaria provoca degli effetti reali nei periodi successivi al primo, che possono essere introdotti riducendo progressivamente i parametri esogeni del tasso di investimento reale e dell’occupazione46, e si può anche presumere che il minor investimento determini una caduta della produttività p. L’idea è quindi quella di partire dalla soluzione di controllo del §1.2.2.1 e di esaminare sei periodi successivi in cui le variabili esogene del modello della Figura 1 prendono rispettivamente i valori dati nella Figura 6.
Figura 6: Scenario della finanziarizzazione: ipotesi sulle esogene
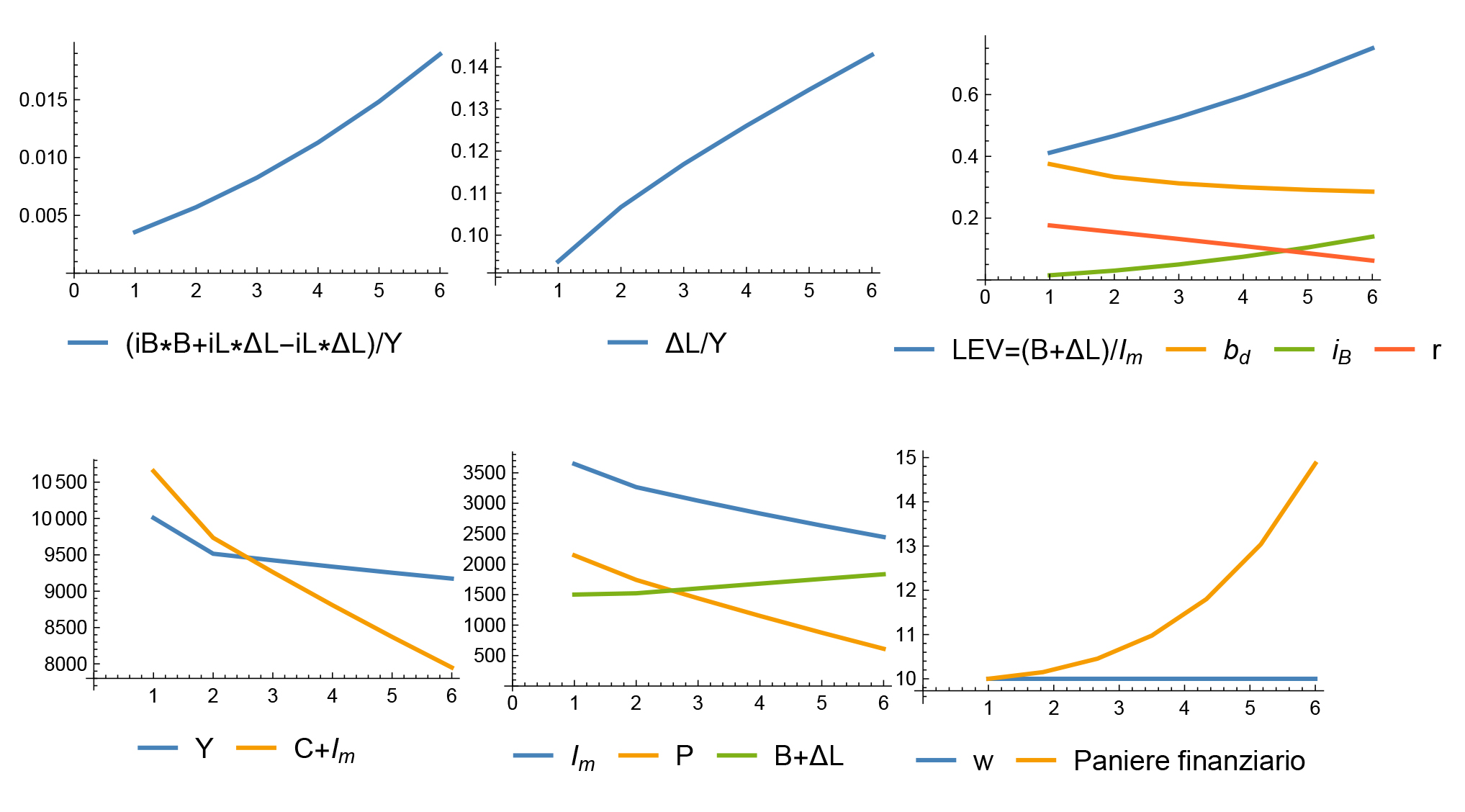
I risultati di questa simulazione sono illustrati dai grafici 18. Il primo mostra che gli interessi aumentano in percentuale del reddito delle famiglie dallo 0,4% al 1,9%, mentre il secondo illustra che la variazione di liquidità passa dal 9% al 14% del reddito. Nel terzo si vede che la leva, definita come rapporto fra la somma della variazione dei debiti delle imprese verso le banche e le famiglie divisa per l’investimento nominale, aumenta dal 41% al 75%, malgrado la riduzione del coefficiente di preferenza delle famiglie per il debito a risparmio bd. Il tasso di profitto scende, poiché b si è ridotto e s è rimasto costante. Come si vede nel quarto grafico, lo scenario è caratterizzato anche da una tendenza alla riduzione del reddito delle famiglie e della domanda finale a prezzi nominali, e da una sostanziale stagnazione di reddito e consumi in termini reali (grafico non riprodotto). Nel quinto grafico si vede che gli investimenti cadono e i profitti ne rappresentano una parte sempre meno rilevante, il saldo essendo dato dalla somma del debito verso le banche (DL) e verso le famiglie (B). L’ultimo grafico illustra infine che a livello di distribuzione del reddito, un paniere di beni uguale inizialmente al salario nominale di dieci, ma investito in un indice finanziario crescente al ritmo del tasso di interesse sulle obbligazioni, varrebbe quindici dopo sei periodi, mentre per ipotesi il salario, fissato a dieci, è rimasto costante.
Grafico 18: Scenario della finanziarizzazione: risultati sulle endogene
In conclusione, i test econometrici condotti nel 2008 per i paesi Visegrad hanno validato empiricamente la teoria del circuito monetario per questi paesi, cosa non del tutto ovvia a priori, trattandosi di economie allora e forse tuttora in transizione. Peraltro, posto che ciò che differenzia il circuito dagli approcci mainstream è l’aggiunta di un terzo polo bancario che crea moneta in maniera autonoma in funzione della redditività dei flussi di liquidità scontati dei vari investimenti possibili47, l’esame di vari indicatori conferma che la teoria del circuito monetario è utile per capire le principali evoluzioni macro-finanziarie recenti e in particolare la caduta del prezzo relativo del lavoro rispetto a quello del risparmio a lungo termine che è poi una delle manifestazioni più significative della cosiddetta finanziarizzazione. Questa è legata all’aumento del valore degli stock finanziari raggiunto attraverso finanziamenti a leva che li privilegiano rispetto ai flussi legati alla produzione come i salari, meno appetibili per la finanza iniziale. Anche senza le modifiche minime che sarebbero necessarie, da esaminare in lavori futuri, il modello del circuito di Graziani riesce a riprodurre e quindi permette di capire molti di questi aspetti della finanziarizzazione.
3. Il legame con la teoria del valore
Oltre al suo interesse teorico discusso nella prima parte e la sua capacità pratica a descrivere e spiegare un certo numero di fatti empirici, discussa nella seconda parte, l’interesse del circuito è anche quello di fornire un legame con la teoria del valore, che, come nella Teoria generale di Keynes, è un valore espresso in unità di salario (Graziani, 1983b), punto più volte sottolineato da Bellofiore (1989, 2018). Si accenna brevemente in quest’ultima parte al fatto che questo legame può servire a costruire un’analisi costi benefici “eterodossa”. Infatti, la non-neutralità della moneta circuitista implica anche una distinzione logica fra prezzi di conto, da usare per valutare l’impatto sociale degli investimenti finanziati, e prezzi di mercato, espressi in contanti.
Dando per scontato che il risultato neoclassico del rendement social di Allais (1943, 1981) è corretto, la variazione di benessere associata a un cambiamento dell’economia è data sostanzialmente dal prodotto delle quantità “incrementali” DQ per un prezzo “di conto” PC:
Per Allais, questo prezzo deve essere quello di mercato, che si suppone uguale al prezzo neoclassico di equilibrio48, ma in altri approcci può essere un prezzo diverso. Ad esempio, la moneta endogena, che nel circuito è non-neutrale, porta a rifiutare l’idea che i prezzi relativi di equilibrio neoclassici possano essere dei prezzi di mercato49. DQ è invece un “fatto” empirico da accertare caso per caso. Il problema per la valutazione sta nel calcolo di PC.
Il circuito si fonda sull’eguaglianza temporale e istantanea tra il valore V(Xt) della produzione Xt realizzata in un lasso di tempo dato e il valore dei redditi monetari creati per remunerare il lavoro impiegato a questo fine all’inizio di questo periodo. C’è quindi una corrispondenza temporale tra la moneta flusso creata al tempo t per fini produttivi DMt e il valore “sociale” V del flusso di beni prodotti durante quel periodo:
relazione che assomiglia a quella della teoria quantitativa della moneta ma che ha un’interpretazione totalmente diversa, poiché si riferisce appunto alla moneta-reddito creata a inizio periodo (finanza iniziale) e non allo stock di moneta accumulato a fine periodo (o alla sua variazione) che fa parte della finanza finale. Incidentalmente, quest’aspetto rivela anche il legame logico fra moneta e investimento netto, poiché, come la moneta, l’investimento è creato e accumulato nel periodo del circuito ed è quindi al tempo stesso un flusso e una variazione di stock.
Anche se non ci sono molti studi teorici né empirici che affrontano la questione da questo punto di vista, si possono prendere come punto di partenza i lavori di Vallageas (1976, 2010, 2018) che si propongono di correggere i prezzi “di produzione di mercato”, per il fatto per esempio che i profitti, nell’interpretazione di Schmitt a cui Vallageas si rifà sotto quest’aspetto, sono un puro trasferimento. La contabilità in “valore-salario” che egli sviluppa ha per effetto di correggere i prezzi di mercato e trasformarli in prezzi espressi in “valore-lavoro” e quindi apre una via che sotto certi aspetti si ricongiunge con l’auspicio espresso da Lesourne (1977) di sviluppare un’analisi costi-benefici espressa unicamente in termini di valore del tempo e che offre inoltre collegamenti suggestivi con la teoria classica del valore-lavoro 50. Infatti, una volta chiarito meglio il legame fra valore della moneta creata per la produzione corrente e quello della moneta che finanzia l’acquisto di attività reali e finanziarie esistenti durante lo stesso periodo (cf. discussione nella seconda parte), lavoro che resta in gran parte da sviluppare, si può pensare a integrare gli schemi del circuito con quelli che discendono dall’interpretazione della teoria del valore-lavoro accolta da Pasinetti (Pasinetti & Garbellini, 2015). Questa linea di indagine si preannuncia difficile e laboriosa ma è molto interessante e potenzialmente feconda di risultati utili. Si può avvalere anche della riflessione avviata da tempo su questi temi da Riccardo Bellofiore (1989, 2018).
Nel modello del circuito monetario:
- Le banche e la moneta hanno esistenza e funzioni proprie. Il modello è particolarmente adatto per interpretare realisticamente fenomeni monetari legati a nuovi prestiti o impieghi.
- C’è un fondamento macroeconomico della microeconomia. “I prestiti creano i depositi” e altre proposizioni collegate, che implicano catene di causalità alternative per valutare gli effetti della politica economica monetaria e finanziaria, sono verificate e/o verificabili empiricamente. Il modello può servire anche a spiegare la formazione di rendite finanziarie.
- Al centro dell’analisi c’è il legame tra prestiti, moneta, investimento e distribuzione del reddito che è cruciale per capire gli effetti sociali della politica economica. Si sa che, fuori dall’equilibrio neoclassico, allocazione e distribuzione non sono indipendenti, ciò che richiede un’impostazione economica del problema della distribuzione che sia aperto rispetto ad analisi multidisciplinari che ne spieghino gli aspetti extra-economici (Roncaglia, 2024). A questo scopo, il circuito suggerisce l’uso di quadro di riferimento basato sulla teoria del valore-lavoro per valutare l’effetto sociale delle operazioni bancarie.
- Nella versione che ha sviluppato Graziani in maniera autonoma e originale51, il circuito è compatibile con quello degli altri autori capostipiti dell’approccio che sono principalmente Schmitt, Parguez e Poulon, i quali giungono a risultati complementari dal punto di vista della politica economica.
In conclusione, per tutte queste ragioni, il circuito monetario è un approccio che appare ineludibile per valutare gli effetti economici e sociali dell’attività bancaria ed è quindi uno schema di indubbia utilità che va approfondito e sviluppato.
Sia consentito in chiusura un commento su come inquadrare il circuito nel resto della produzione scientifica e culturale di Augusto Graziani. Graziani è stato un economista completo col pallino della macroeconomia e un grande esperto di moneta e politica monetaria. Ha affrontato tutti i problemi più difficili della teoria economica armato della sua grande cultura e profonda conoscenza della storia del pensiero economico, nutrita dalla sua lettura attenta dei classici economici condotta in lingua originale. Fin dall’inizio della sua carriera di docente, si è interessato ai problemi di analisi costi benefici (Graziani, 1961) con largo anticipo sui primi manuali che l’OCSE e la Banca Mondiale dedicheranno al tema alla fine degli anni Sessanta, restringendolo progressivamente al solo ambito neoclassico. Il suo rigore intellettuale lo ha portato a rigettare l’analisi neoclassica del capitale già nel 1965, contribuendo indirettamente e in maniera discreta a nutrire un dibattito importante e generalmente trascurato che ha coinvolto all’epoca i principali economisti neokeynesiani e post-keynesiani delle due sponde dell’atlantico (Graziani, 1965, discusso in Cingolani, 2016).
Ma la sua mente fertile non si interessava solo di questioni teoriche. Oltre a formare diverse generazioni di studenti, molto dei quali sono diventati a loro volta docenti o dirigenti in Italia e all’estero, dedicava grande attenzione alla storia (Graziani, 1975) ed è stato un cittadino fortemente impegnato nel dibattito politico e civile. In particolare, ha dedicato molte delle sue energie ad affrontare concretamente i difficili problemi dello svilluppo del Mezzogiorno italiano (Graziani, 2020) animando tra l’altro insieme a Rossi la celebre scuola di Portici (Costabile, 2004) che ha contribuito a formare una parte rilevante della classe dirigente economica nazionale.
È probabilmente dal confronto tra l’osservazione attenta della realtà nelle sue sfaccettature più problematiche e la sua profonda conoscenza della dottrina economica che è nata l’intuizione del circuito monetario che è uno dei suoi contributi più originali e fecondi. Come si è cercato di mostrare, questo schema offre una chiave semplice e rigorosa per ragionare sui fatti monetari e finanziari, che ha rilevanza empirica e molte possibilità di sviluppo future.
1 Banca europea per gli investimenti. Le idee espresse lo sono a titolo personale. Testo scritto per il blog del sito dedicato ad Augusto Graziani (Blog Graziani) che rielabora una presentazione online per la Rete Italiana Post-Keynesiana nel quadro di una “Lezione sul pensiero di Augusto Graziani” organizzata con Riccardo Bellofiore l’ 8.4.2022 (IPKN Lezione Graziani). Il testo derivato da questa presentazione è stato poi discusso in un convegno a Bordeaux il 6-7 dicembre 2022 (“Circuit et modélisation macro-économique de la transition écologique: I. Fondements et actualité du circuit”). Versioni precedenti di questo testo hanno beneficiato di commenti e/o incoraggiamenti da parte di Riccardo Bellofiore, Eric Berr, Marcella Corsi, Jean-Paul Guichard, Marc Lavoie, Luca Lazzaroli, Eugenio Leanza, Edwin Le Héron, Matthieu Llorca, Fréderic Poulon, Louis-Philippe Rochon, Sergio Rossi, Mario Seccareccia e Bernard Vallageas che sono calorosamente ringraziati. L’autore resta responsabile di tutti gli errori rimanenti. Versione originale italiana datata 24 novembre, 2024.
2 In questa definizione, de Finetti non si sofferma sulla distinzione che si fa talvolta, specie nella letteratura antropologica, fra moneta e denaro. Si ringrazia Riccardo Bellofiore per avere segnalato all’autore che anche Graziani (1983a, p. 225) fa questa distinzione, che introduce per illustrare il concetto marxiano di moneta come equivalente generale, per cui egli contrappone la ricchezza in generale (denaro, Geld in tedesco) alla liquidità (inclusiva di “contante” o Münze in tedesco, e per estensione di “depositi”, Einleigen in tedesco). La distinzione tra i due concetti è importante e molto attinente al tema qui trattato, ma si può osservare che i principali dizionari italiani tendono a trattare denaro e moneta come sinonimi riprendendo l’uso della lingua parlata. Comunque, accogliendo questa distinzione, per de Finetti le operazioni finanziarie hanno per oggetto lo scambio di liquidità (contante e depositi) o flussi di cassa.
3 Non è del tutto ovvio definire cos’è il mainstream (o pensiero egemonico) in economia, eccetto che come l’insieme di dottrine che più incidono sulle decisioni collettive. Un punto che accomuna questi approcci, che a bene vedere sono molto diversi fra loro, è che tendono a interpretare normativamente i prezzi di mercato, e quindi considerarli come prezzi “naturali”, per cui la distribuzione dei redditi e delle ricchezze diventa un dato esogeno che esula di fatto dall’analisi economica. Riccardo Bellofiore ha osservato che le politiche odierne sono soprattutto ispirate alla scuola austriaca che è per lui eterodossa. Certamente molti degli autori “neo-austriaci” si considerano e vengono considerati eterodossi; tuttavia, Hayek resta pur sempre uno dei tre capostipiti dell’equilibrio economico generale moderno e quindi a giudizio di chi scrive la sua scuola si può annoverare nel mainstream. Peraltro, nella vulgata economica dominante si mescolano in un unico calderone elementi neoclassici, monetaristi e neo-austriaci, generando una confusione che rende il dibattito economico totalmente incomprensibile al pubblico non specialistico. Uno dei pochi punti di accordo è appunto lo slogan: “You have got to get your prices right”, dove per “right” si intende “prezzi di mercato”.
4 Nel testo si parla soprattutto di famiglie piuttosto che di lavoratori e di imprese piuttosto che di capitalisti seguendo la terminologia in uso in contabilità nazionale. Per quanto, come rileva Riccardo Bellofiore, questa terminologia non sia a rigore applicabile al modello di Graziani, dove i settori coincidono con le classi sociali degli economisti classici, il riferimento alla contabilità nazionale è giustificato perché da un lato lo sviluppo del circuito monetario è sempre stato molto legato ed ha influenzato quello della contabilità nazionale e dei flussi di fondi, specie nella tradizione francese (Denizet, 1972; Poulon, 2015, pp. 95-150, Berr & Monvoisin, 2023), e dall’altro qualsiasi verifica empirica del circuito poggia sui concetti e aggregati di contabilità nazionale.
5 Nei modelli neoclassici che integrano le banche, queste svolgono un ruolo passivo di intermediazione fra il risparmio e l’investimento (Graziani 2003a, pp. 74-81). La moneta è uno stock la cui creazione è devoluta al solo settore pubblico che la realizza attraverso i disavanzi di bilancio (Graziani, 1984a, p. 127). Da qui deriva l’idea che ha dominato le politiche economiche occidentali dopo gli anni Settanta di ridurre il deficit pubblico per evitare l’inflazione di origine monetaria. Come proposto da Milton Friedman, lo scopo era quello di stabilizzare la quantità di moneta in circolazione controllando il tasso di crescita della base monetaria, che avrebbe dovuto rimanere costante. Queste politiche sono state abbandonate abbastanza rapidamente perché si sono rivelate impossibili da mettere in atto, ma le idee che le sottendono restano dominanti, come testimoniano i dibattiti odierni sull’inflazione.
6 In macroeconomia un modello si compone generalmente di un certo numero di equazioni che legano fra loro variabili diverse, alcune spiegate dal modello stesso, altre considerate come date. Un blocco all’interno di un modello corrisponde a un sottogruppo di equazioni che tratta fenomeni collegati, ad esempio il blocco del consumo, quello della produzione o quello dei prezzi e dei salari. In genere le equazioni di un blocco sono logicamente distinte dalle altre e la loro soluzione può essere esaminata indipendentemente da quella del resto del modello (Deleau e Malgrange, 1978). Nella generazione dei modelli macro-econometrici Keynesiani degli anni Settanta, che ha svolto un ruolo importante nella gestione economica delle trente glorieuses, il blocco monetario e finanziario era notoriamente il più carente. Constatata la difficoltà di questi modelli a spiegare la moneta e la macro-finanza, a partire dagli anni Ottanta si è pensato di escludere totalmente la moneta e le banche dai modelli macro-econometrici, come si fa nei modelli cosiddetti DGSE (Dynamic Stochastic General Equilibrium) tuttora in uso presso diverse banche centrali e istituzioni internazionali. Piuttosto che ignorare la moneta, un’alternativa più feconda sarebbe stata invece quella di seguire la via indicata da Graziani e introdurla all’interno di questi modelli a partire da una comprensione dettagliata del suo funzionamento. Va precisato a riguardo che, malgrado i loro limiti teorici, le proiezioni dei modelli DGSE possono comunque essere attendibili, e per questo vengono usate, dato che è sempre possibile calibrare il modello con una tolleranza data rispetto alle rilevazioni empiriche e questo consente di fare previsioni ragionevolmente attendibili nel breve termine. Il problema è però che quando questi modelli vengono usati per la simulazione di scenari in variante, trascurano quella parte ignota del meccanismo di trasmissione della politica monetaria che è inclusa nel fattore di aggiustamento usato per calibrare il modello, che è poi il “residuo” (diverso da zero) usato in proiezione per ottenere la simulazione di controllo (“la previsione”), talvolta indicato anche come “add-factor”.
7 Ovviamente né Graziani, né i principali circuitisti e post-keynesiani o i neoclassici lo hanno mai fatto.
8 La versione “insiemistica” o anche “topologica” dell’equilibrio generale si riferisce al modello di Arrow-Debreu. È più astratta e usa una matematica meno comprensibile di quella tradizionale neoclassica di Walras e Pareto, basata su modelli a equazioni simultanee, ma conferma e specifica più rigorosamente il campo di validità dei suoi risultati.
9 Al contrario e tipicamente nei modelli neoclassici, la macroeconomia è data dalla somma dei comportamenti microeconomici individuali (Malinvaud, 1956), il che preclude in ultima analisi ogni possibilità di disoccupazione involontaria. Per un collegamento con la controversia sul capitale, si veda Seccareccia (1982).
10 Generalmente illustrata dicendo che non sono le stesse persone le quali risparmiano e investono, che sono gli investimenti che creano i risparmi, o che il risparmio liquido del singolo, a lui benefico, è un danno per la collettività.
11 Anche se i modelli simultanei sono usati regolarmente per discutere di politica economica, in realtà non si sa quale variabile causa quale altra, dato che tutto avviene allo stesso tempo, eccetto nel caso abbastanza raro in cui sono totalmente ricorsivi e quindi sequenziali sul piano logico (Pasinetti, 1965).
12 L’autore è in debito con Riccardo Bellofiore per avergli segnalato questa introduzione, come quella altrettanto fondamentale al libro di Convenevole (Graziani, 1977).
13 “Equilibrio” va qui inteso nell’accezione di “soluzione del modello” (Deleau & Malgrange, 1978) e quindi non implica necessariamente il raggiungimento delle condizioni competitive neoclassiche di tipo “prezzo=costo marginale”. Nel circuito di Graziani, al di fuori di un’eguaglianza fortuita fra l’investimento e il risparmio, l’equilibrio può coincidere solo con la costanza (o variazione nulla) delle scorte liquide. L’autore è grato a Louis-Philippe Rochon per aver insistito sulla necessità di chiarire questo punto.
14 Questo è il motivo per cui i tentativi di fornire fondamenti microeconomici al circuito, come quelli di Messori (1988) e Bossone (2001), non possono essere davvero qualificati come circuitisti, nonostante l’interesse dei loro risultati. Schmitt e la scuola di Digione-Friburgo hanno stabilito senza dubbio che il ‘flusso circolare’ (o circuito) può essere solo macroeconomico, e Graziani, Parguez e Poulon sostengono questa posizione.
15 Sia consentita una piccola digressione. Le formulazioni originali della teoria di Kalecki in polacco e in tedesco precedono la Teoria Generale, ciò che ha fatto dire ad alcuni esperti che Keynes avrebbe “copiato” Kalecki su questo punto. Altri esperti obiettano che dato che Keynes non parlava né polacco, né tedesco, le scoperte di questi due maestri sono state indipendenti. L’autore è grato a Jean-Paul Guichard per avergli segnalato che se Keynes non avesse capito il tedesco, non avrebbe potuto scrivere il Trattato sulla Probabilità (che in effetti discute in dettaglio tutta la letteratura probabilistica e attuariale tedesca dell’Ottocento), e che le idee principali di Kalecki erano state presentate nel 1935 in francese a un congresso della società di econometria al quale Keynes aveva partecipato. Non si può quindi escludere che Keynes fosse venuto a conoscenza delle idee principali di Kalecki, anche se parlare di plagio è forse eccessivo.
16 Graziani (1983 e 1984a) argomenta che questa separazione differenzia i due principali filoni della letteratura monetaria che si possono ricondurre a Fisher e Friedman da un lato, che sostengono che l’interesse monetario si adatta pienamente all’inflazione, e dall’altro a Wicksell, Keynes e Robertson, che contestano la veridicità dell’indicizzazione totale dei tassi di interesse all’inflazione.
17 Per usare la tassonomia proposta da Musgrave (1981), citato da Salanti (1985), ignorare le variazioni delle scorte liquide, è, come mostra il modello del circuito, un’ipotesi “non-trascurabile” (“non-negligible”), nel senso che il suo abbandono modifica la causalità fra le principali variabili macroeconomiche (Cingolani, 2022, p. 256 e seguenti).
18 Come osservato, per il circuito, la moneta è una passività emessa da un terzo estraneo alla transazione (acquisto o vendita) che viene accettata dalle due parti proprio perché il terzo (Stato, banche, o persona facoltosa) è un’entità esterna alla transazione e quindi “credibile”. Questa definizione esclude che i cosiddetti “I Owe You” siano moneta, non si può cioè pagare con proprie promesse di pagamento o, se si fa, queste non sono moneta. Per la stessa ragione, i bitcoins non sono moneta in senso circuitista perché sono un’attività e non una passività, sono cioè beni che hanno un valore più o meno permanente, sia esso speculativo (materie prime), collezionistico (francobollo) o artistico, ma che non deve normativamente scomparire al momento della chiusura del circuito, come fa la moneta circuitista.
19 Parguez parte da un modello minimo in cui figura anche lo Stato, perché per lui senza di esso non si può concepire lo “spazio della moneta”. Graziani invece, seguendo in questo il modello di credito puro del neoclassico Wicksell, fa la scelta più radicale di iniziare il ragionamento da uno schema in cui c’è solo il settore privato, ciò che gli permette di illustrare come la classe sociale dei capitalisti, avendo accesso al credito, decide l’allocazione delle risorse fra consumo e investimenti. Parguez, e in generale i circuitisti francesi, ammettono l’esistenza di una moneta di “secondo rango” emessa dalle banche private a favore dei capitalisti, ma questa è logicamente (perché legalmente) inferiore alla moneta di primo rango emessa dalla banca centrale, che è la sola “vera moneta”. La gerarchia fra moneta di primo e di secondo rango (base monetaria e M1), non viene contestata da Graziani, ma l’adozione di un’ipotesi teorica più drastica, gli permette di illustrare le condizioni minime per l’esistenza della moneta, fra cui non include l’esistenza dello Stato. Si trovava comunque probabilmente d’accordo con Parguez quando questi ironizzava sul fatto che il debito pubblico è “oro” per l’attivo di bilancio di una banca, come aveva a suo tempo osservato il banchiere, parlamentare francese e fondatore del Crédit Lyonnais Henri Germain (Cingolani, 2013).
20 Graziani (1985) discute il caso col settore pubblico, mentre Graziani et al. (1969) può essere considerato una descrizione del circuito in economia aperta.
21 Modigliani e Cohn (1979) discusso in Graziani (1984a).
22 Questo raggruppamento delle equazioni non c’è come tale in Graziani, che affronta separatamente i problemi della produzione e della distribuzione nel capitolo V, e quelli della circolazione del risparmio nel capitolo VI, ma è una conseguenza relativamente ovvia della sua analisi. Questa inizia con le relazioni del capitolo IV che introduce i due seguenti esaminando la creazione monetaria da parte del settore bancario. Esplicitare il modello della Figura 1 consente di illustrare il funzionamento del blocco monetario e finanziario del circuito che, integrando la moneta endogena, ribalta le relazioni causali dei principali modelli macroeconomici quando viene ad essi integrato. A rigore, le 14 equazioni della Figura 1, che corrispondono esattamente a quelle dei capitoli V e VI del testo del 2003 relative ai due blocchi della distribuzione e della finanza (che descrivono schemi complementari di “equilibrio parziale”), andrebbero completate esplicitando i flussi di rendita da interesse fra il polo bancario e le famiglie, poiché di fatto in queste equazioni ci sono solo due tipi di percettori di reddito: le famiglie e le imprese. Ma, come argomentato nel testo, se si interpreta il settore produttivo come il consolidato di banche e imprese, l’interesse pagato dalle imprese alle banche e alle famiglie è incluso nei profitti dei produttori, mentre si può trascurare l’interesse pagato sui depositi purché il suo livello sia sufficientemente basso. È questa la scelta fatta in questa sezione per aderire più fedelmente possibile al testo di Graziani.
23 Cioè tutta la produzione è ridotta a quantità datate di lavoro. Si ringrazia Eugenio Leanza per aver insistito sulla necessità di esplicitare quest’aspetto.
24 Come giustamente fatto rilevare da Marc Lavoie, se il livello dell’occupazione N, come quello della produttività p sono dati, in effetti è dato anche il livello della produzione X che non è quindi strettamente endogeno. Oltre che per disporre di una relazione che rispetti la linearità dei coefficienti di produzione assunta da Graziani come da molta della letteratura post-keynesiana, si è scelto di trattare l’output come endogeno e l’impiego come esogeno per evidenziare che nel circuito di Graziani le imprese decidono sia il livello dell’occupazione e quindi della produzione, che la sua ripartizione fra beni di consumo e beni di investimento. Si potrebbe dire che le imprese hanno l’imbarazzo della scelta fra le variabili che sono sotto il loro controllo per definire ogni aspetto del ciclo di produzione e distribuzione. Tale libertà deriva dal fatto che le banche mettono a loro disposizione il potere d’acquisto necessario per realizzare i propri piani. Le famiglie lavoratrici non hanno invece un simile accesso al credito per la creazione di reddito. Possono solo decidere il livello del loro risparmio come frazione del reddito che le imprese e le banche hanno deciso di distribuire loro. Le imprese sono a loro volta di fatto subordinate al settore bancario al quale devono destinare una parte dei profitti sotto forma di interessi. Al conflitto capitale lavoro per la ripartizione tra salari e profitti, si sovrappone quindi, e in effetti prevale in Graziani, quello fra imprese e banche per la ripartizione fra profitto e interesse.
25 Graziani (2003, p. 102) osserva che il livello dei prezzi non dipende dalla quantità di moneta, che è totalmente endogena nel circuito.
26 Lettura che Alain Parguez considerava insuperata (comunicazione personale).
27 Questa perdita non appare nella relazione (9) perché il settore produttivo è il consolidato di banche e imprese, si veda nota 36.
28 Il che dimostra en passant l’interesse della scomposizione in fasi del periodo di produzione del circuito fatta da Graziani.
29 In effetti compatibile a sua volta con gli schemi di riproduzione di Marx, ciò che non dovrebbe sorprendere più di tanto alla luce dell’analisi di Barone (1908).
30 È noto che Kalecki non abbia mai scritto questa frase che gli è stata attribuita da Kaldor e Robinson.
31 Nelle relazioni (10) e (12) i coefficienti b e m sono al tempo stesso dei parametri di scala e di comportamento. Si può infatti mostrare che per assicurare che la proporzione di risparmio investita in titoli bd=bs sia compresa fra zero e uno bisogna che prevalgano le seguenti condizioni fra le variabili di questo blocco: ß>√iB /)iD e μ>iL⁄√iB.
32 In effetti la (10) si può ricavare da bd=iB ⁄ [ß2 iD2 ] per la domanda di risparmio in titoli delle famiglie e da per l’offerta di titoli delle imprese ponendo bd=bs.
33 In questo caso, la condizione di equilibrio sul mercato finanziario che postula l’eguaglianza fra domanda e offerta di titoli delle imprese in proporzione al risparmio (che Graziani scrive genericamente: bd[iB/iD]=bs[iL/iB]=b) è posta uguale a uno (Graziani, 2003a pp. 124 e p. 127), il che implica anche una variazione nulla delle scorte liquide. Il caso è dunque quello di “moneta senza crisi” (Graziani, 1984b) e non quello “Malthusiano” (Graziani, 1980), in cui la moneta spiega il principio della domanda effettiva.
34 Fra le esogene si potrebbe a rigore distinguere i parametri di comportamento o tecnologici (b, s, ß, µ, e ∏), dal resto delle esogene (N, iD, iL, w), ma qui i due gruppi di variabili sono trattati congiuntamente dato che i loro valori sono assunti come costanti e determinano insieme il valore delle variabili endogene.
35 La soluzione rispetta le identità seguenti: p*X = C+Im = W + P + iBB; Y = C + S = W + ΔL; S=B+ΔL; Im = S + P. Le prime tre identità esprimono la triplice definizione del reddito nella contabilità nazionale. Se si considera il polo della produzione come il consolidato delle imprese e delle banche, il suo profitto P, include anche quello delle banche, che è un reddito che non va alle famiglie e che rappresenta quindi un trasferimento interno al polo della produzione quando questo è consolidato. Tuttavia, dato che iB*B non è incluso in W, bisogna aggiungerlo a W e P per ritrovare la definizione del prodotto nell’ottica dei redditi. A rigore, l’interesse pagato dalle banche sui depositi delle famiglie andrebbe aggiunto al reddito delle famiglie Y, se non fosse che qui si può trascurare perché è posto praticamente a zero nelle simulazioni effettuate. La necessità di questa correzione quando iD è nettamente superiore a zero risulta dalla scelta di mettere insieme le equazioni dei capitoli V e VI di Graziani (2003a), ma non è un requisito logico per il testo originale, che è adatto ad esaminare separatamente la problematica della distribuzione e della circolazione.
36 La figura corrisponde a quella presentata da Graziani (2003a, p. 127).
37 L’esplicitazione del conflitto distributivo fra banche e imprese è uno dei contributi più interessanti e fecondi dell’analisi di Graziani e gli ha consentito di dimostrare come l’identità di Fisher secondo la quale il tasso di interesse nominale sarebbe la somma del tasso di interesse reale e del tasso di inflazione non è necessariamente valida a seconda che la creazione monetaria venga dal deficit pubblico oppure dalla creazione di moneta bancaria (Graziani, 1983a e 1984a), risultato tutt’altro che ovvio e sulla sottilità del quale l’attenzione dell’autore è stata attirata a suo tempo da Alain Parguez.
38 Il materiale presentato in questa sezione è stato preparato per una tavola rotonda del SIOI nel 2017 e per questo motivo i dati esaminati arrivano al 2016. “Riflessioni su moneta e finanza nello spazio europeo”, Tavola rotonda su L’Europa a geometria variabile: aspetti economici, monetari e di sicurezza, 3 ottobre 2017, Roma: SIOI. È poi stato usato anche in conferenze svoltesi lo stesso anno a Venezia e a Grenoble. “Financial assets dynamics in industrialized countries: trends and implications: A critical review of the financial balance sheets of the main industrial countries”, Interest Rates, Growth and Regulation, Venezia: 28-29 settembre 2017; e: “Financial assets dynamics in industrialized countries: trends and implications”, International Post-Keynesian and Institutionalist Conference on “Instability Growth & Regulation”, Grenoble: December 7-9, 2017.
39 Perché ciò avvenga basta che il “tempo” del circuito finanziario sia più breve di quello del circuito “reale”, come elaborato nei paragrafi del §2.2 e §2.3. Si ammette quindi implicitamente che in un dato periodo si possano svolgere due circuiti: quello “canonico” o “industriale”, relativo alla generazione del reddito (ricchezza reale) e quello finanziario “degli scambi di denaro “. Quest’idea è sviluppata schematicamente in Cingolani (2013b, p. 283) e in Cingolani (2019, p. 283) dove viene usata per discutere e interpretare rispettivamente l’evoluzione delle variabili macro-finanziarie europee e il ruolo della banca pubblica. In Cingolani (2024, pp. 811-14) si sviluppa invece un esempio di articolazione delle fasi del periodo singolo del circuito per discutere il problema del finanziamento privato delle attività ambientali. Di recente l’autore è venuto a conoscenza del ricco contributo di Bradley (2001) che tratta del circuito dei redditi e a quello del capitale mostrando come la distinzione fra i due, implicita in Graziani e negli altri fondatori del circuito perché svolgono l’analisi nel periodo singolo, si può far risalire al dibattito fra Currency School e Banking School al momento dell’introduzione del Banking Act del 1844 nel Regno Unito, dibattito a cui Graziani fa frequenti riferimenti.
40 Si è scelto questo valore iniziale arbitrario come parametro per distinguere meglio le curve sul grafico in funzione delle rispettive scale.
41 A rigore il paragone porta su la velocità delle dinamiche del valore di mercato, ma accettando un’ipotesi semplificatrice di omogeneità dei panieri di “quantità” di tali attivi, si può attribuire la maggior parte della variazione dei valori relativi ai prezzi di queste attività, anche perché nel campo dei prodotti finanziari non ha molto senso distinguere la quantità dal prezzo.
42 Guardando ai flussi di finanziamento lordi, si ha un’indicazione della finanza “inizialmente consentita” ma in genere non si osservano i prestiti richiesti inizialmente dalle imprese ma a loro rifiutati dalle banche, quelli cioè che rappresentano la loro “vera” percezione della domanda effettiva.
43 Come osservato nella sezione precedente, si veda anche Cingolani (2013a).
44 Originariamente, questo tipo di correlazione è stata studiata da Moore (1988).
45 Ovviamente, se si aggiungessero della equazioni relative agli stock di titoli accumulati in passato, la rendita sarebbe molto più alta poiché lo stesso tasso di interesse si applicherebbe allo stock di titoli delle imprese e non alla sua variazione. Trascurando gli stock, si fa di fatto un’ipotesi implicita che i titoli emessi dalle imprese hanno una durata di vita pari a quella del circuito, oppure si assume, come fa Graziani, che ci si trova nel periodo singolo iniziale, in cui questi stock sono ancora nulli perché mai accumulati. In tal caso si puo’ guardare al circuito come un modello a due periodi alternativo a quallo neoclassico delle generazioni sovrapposte sviluppato da Allais (1947) e Samuelson (1958).
46 La riduzione del tasso di investimento e la minor crescita o la riduzione dell’impiego sono tipicamente associate alla finanziarizzazione. Per il tasso di investimento, si vedano ad esempio i grafici 22-30 a pp. 277-81 di Cingolani (2013b).
47 Cioè in maniera “endogena” rispetto al funzionamento del sistema economico e ai suoi bisogni di liquidità.
48 Anche se in genere non entra esplicitamente in queste discussioni, sembra lecito affermare che Allais, uno dei massimi teorici dell’analisi del welfare, presume l’applicabilità al mondo reale dell’ottimo di primo rango (first best), che è di equilibrio in quanto risultante da una massimizzazione vincolata e, essendo “ottimale”, induce a ritenere che qualsiasi deviazione rispetto a quest’ottimo sia “di secondo ordine”. Nelle analisi empiriche sui costi-benefici, si tende invece a separare prezzi di conto (o prezzi ombra) e prezzi di mercato, cosa che è in contraddizione con la finanza odierna che postula invece possibilità di arbitraggio infinite, oppure, quando ammette che queste possibilità non sono infinite, non guarda alle conseguenze sistemiche di un aumento delle rendite a scapito dei profitti. A rigore, andrebbe aggiunto che, nell’interpretazione di Schmitt, lo scambio iniziale salario-lavoro è assoluto e non relativo, e quindi i prezzi che ne derivano sono anch’essi assoluti e non relativi, ma sviluppare quest’aspetto richiederebbe spazi molto più ampi (si veda Schmitt, 2012).
49 Come osservato, nell’equazione (1) della Figura 1, lo sono quando b=s.
50 Il fatto che la liquidità creata dai prestiti nel finanziamento iniziale rappresenti i redditi salariali prefigura una possibile integrazione con la teoria del valore-lavoro sviluppata da Pasinetti (1986 e 1993) sulla scia delle analisi di Sraffa. Si veda anche il recente contributo di Giraud (2024).
51 Come ben spiegato da Riccardo Bellofiore nella sua lezione Graziani per IPKN e in Bellofiore (2013 e 2019). In generale, sull’apporto di Graziani, oltre agli eccellenti contributi pubblicati su questo blog, si vedano tra gli altri gli ottimi Fausto (2014), Costabile (2015) e Giannola (2020).
Riferimenti
- Allais, Maurice. [1943] 1994. A la recherche d’une discipline économique, pubblicato col titolo Traité d’Économie Pure, Paris: Clément Juglar.
- Allais, Maurice. [1947] 1998. Economie et intérêt. Paris : Clément Juglar.
- Allais, Maurice. [1981] 1989. La théorie générale des surplus : nouvelle édition précédée d’un avant-propos de l’auteur. Grenoble : Presses Universitaires de Grenoble (première édition : Economies et Sociétés Cahiers de l’ISMEA n. 1 à 5, 1981)
- Barone, Enrico. 1908. “Il ministro della produzione nello stato collettivista”, Giornale degli Economisti, Serie Seconda, Vol. 37 (Anno 19), settembre: pp.267-293. e “[…] Continuazione”, ibid., ottobre: 391-414.
- Bellofiore Riccardo. 1989. “A Monetary Labour Theory of Value”, Review of Radical Political Economics, 21, n. 1-2: 1-25.
- Bellofiore, Riccardo. 1998. “Between Wicksell and Hayek: Mises’ Theory of Money and Credit Revisited”, American Journal of Economics and Sociology, Vol. 57, No. 4 (Oct.), pp: 531-578.
- Bellofiore, Riccardo. 2013. “A heterodox structural Keynesian: honouring Augusto Graziani”, Review of Keynesian Economics, Vol. 1 No. 4 (Winter), pp. 425–430.
- Bellofiore, Riccardo. 2018. Le avventure della socializzazione. Dalla teoria monetaria del valore alla teoria macro-monetaria della produzione capitalistica. Milano: Mimesis.
- Bellofiore, Riccardo. 2019. “Augusto Graziani and the Marx-Schumpeter-Keynes ‘Cycle of Money Capital’: A Personal Look at the Early Italian Circuitism from an Insider”, Review of Political Economy, 31:4, 528-558
- Bellofiore, Riccardo. 2022. “La moneta come capitale. Augusto Graziani e il primo circuitismo: 1975-1985”, Intervento alla Lezione sul pensiero di Augusto Graziani, evento online organizzato dall’Italian Post Keynesian Network il 8.04.2022: IPKN Lezione Graziani.
- Berr, Éric & Virginie Monvoisin. 2023. “Modern post-Keynesian approaches: continuities and ruptures with monetary circuit theory”, Journal of Post Keynesian Economics, 2023, DOI: 10.1080/01603477.2023.2167092
- Bossone, Biagio. 2001. “Circuit theory of banking and finance”, Journal of Banking & Finance, 25: 857-890.
- Bradley, Xavier. 2001. “An experience in banking departmentalisation: the Bank Act of 1844”, Working Papers 5 (Quaderni di ricerca) of the Laboratory of Research in Monetary Economics of the Centre for Banking Studies (CSB) of Lugano-Vezia, Switzerland. Disponibile all’indirizzo: Bradley.
- Cingolani, Massimo. 2013a. “The monetary conditions for growth: Parguez’s debt stability condition”, Ch. 14 in: Monetary Economies of Production. Banking and Financial Circuits and the Role of the State, Louis-Philippe Rochon and Mario Seccareccia ed., pp. 205-234, Cheltenham UK: Edward Elgar.
- Cingolani, Massimo. 2013b. “Finance Capitalism: A Look at the European Financial Accounts”, Panoeconomicus, 2013, 3, Special Issue, pp. 249-290.
- Cingolani, Massimo. 2016. “Augusto Graziani’s Equilibrio generale ed equilibrio macroeconomico: A key milestone in a long journey out of the neoclassical mainstream”, Review of Keynesian Economics, Vol. 4 No. 3, Autumn 2016, pp. 279–302.
- Cingolani, Massimo. 2019. “Necessary Public Investment: The Role of Public Banks”, International Journal of Political Economy, 48:3, 275-300.
- Cingolani, Massimo. 2022. “What Economic Modelling Hypotheses Should Underlie Regulation & Policy Advice? Towards a Probabilistic Approach”, Forum for Social Economics, 2022, Vol. 51, N. 3, 253–284.
- Cingolani, Massimo. 2024. “Public and Private Financing of Sustainable Development Goals (SDGs)”, Review of Political Economy, 36:2, 792-826.
- Costabile, Lilia. 2004. “Il Centro di Specializzazione e Ricerche Economico-Agrarie per il Mezzogiorno e la ‘Scuola di Portici'”, in: La formazione degli economisti in Italia (1950-1975), a cura di Giuseppe Garofalo e Augusto Graziani, Bologna: Il Mulino.
- Costabile, Lilia. 2015. “Augusto Graziani: Theoretician, Applied Economist, Historian of Economic Thought: An Appraisal”, Italian Economic Journal, n. 1 :155–170
- de Finetti, Bruno. [1935] 1991. “Sulle operazioni finanziarie”, Giornale dell’Istituto Italiano degli Attuari, Roma, 1935, Anno VI, n. 4, pp. 289-302 In: Scritti 1931-1936, Bologna: Pitagora editrice.
- Deleau, Michel e Pierre Malgrange. 1978. L’analyse quantitative des modèles macroéconomiques quantitatifs, Paris : Economica.
- Eichner, Alfred S. 1973. “A Theory of the Determination of the Mark-Up under Oligopoly.”, Economic Journal, 83 n. 332: 1184–1200.
- Eichner, Alfred. S. 1991. The macrodynamics of advanced market economies. Armonk, N.Y.: Sharpe.
- Fausto, Domenicantonio. 2014. “Augusto Graziani: a profile”, Studi Economici dell’Università degli Studi di Napoli Federico II, VXIX (112), 10–28, Special issue on ‘The Scientific Work of Augusto Graziani’, riprodotto in Accademia Nazionale dei Lincei.
- Giannola, Adriano. 2020. “Introduzione” ad Augusto Graziani: Mercato, Struttura, Conflitto: Scritti su economia italiana e Mezzogiorno: 11-41.
- Giraud, Pierre-Noël. 2024. Du Pain et des jeux. Une économie politique des usages du temps. Paris : Odile Jacob.
- Graziani, Augusto. 1961. La teoria delle scelte negli investimenti pubblici. Napoli: Casa editrice Dott. Eugenio Jovene.
- Graziani, Augusto. 1965. Equilibrio generale ed equilibrio macroeconomico, Napoli: Edizioni Scientifiche Italiane.
- Graziani, Augusto, Grazia Bagolini, Marinella Balestrieri Terrasi, Giuliana Barchiesi, Gaetano Marenco, Bruno Trezza and Salvatore Vinci. 1969. Lo sviluppo in un’economia aperta, Napoli: Edizioni Scientifiche Italiane.
- Graziani, Augusto. 1975. Crisi e ristrutturazione nell’economia italiana. Torino: Einaudi.
- Graziani, Augusto. 1977. “Recensione a mo’ di premessa”, Introduzione a: Processo inflazionistico e redistribuzione del reddito, R. Convenevole, Torino: Einaudi, XI-LVI.
- Graziani, Augusto. 1980. “Malthus e la teoria della domanda effettiva”, Introduzione a Malthus. Sviluppo e ristagno della produzione capitalistica, Lilia Costabile, pp.: VII-LV, Torino: Giulio Einaudi, Editore, 1980.
- Graziani, Augusto. 1981. “Keynes e il Trattato sulla moneta”, In Studi di economia Keynesiana, 211-234, a cura di Augusto Graziani, Cesare Imbriani e Bruno Jossa, Napoli, Liguori editore.
- Graziani, Augusto. 1983a. “Interesse monetario e interesse reale. Storia di una controversia”, Rivista Milanese di Economia, n. 6: 77-108.
- Graziani, Augusto. [1983b] 1997a. “Moneta e credito nell’economia marxiana”, in: I conti senza l’oste: Quindici anni di economia italiana, Torino: Bollati Boringhieri, pubblicato originariamente su Rinascita, nn. 50-51, 23 dicembre 1983.
- Graziani, Augusto. [1983c] 1997b. “Riabilitiamo la teoria del valore”, I conti senza l’oste, 235-240, Torino: Bollati Boringhieri. Originariamente in L’Unità, 27 febbraio 1983, supplemento speciale per l’anniversario della morte di Karl Marx.
- Graziani, Augusto. 1984a. “Interesse monetario e interesse reale”, In: L’interesse reale e monetario, a cura di Giacomo Costa, Alfredo del Monte, Adriano Giannola, Augusto Graziani, Ferruccio Marzano, Milano: Franco Angeli.
- Graziani, Augusto. 1984b. “Moneta senza crisi”, in Studi Economici, XXXIX, n. 3, 1984, pp. 3-37.
- Graziani, Augusto. 1984c. “The Debate on Keynes’s Finance Motive.”, Economic Notes, n. 1: 15-33.
- Graziani, Augusto. 1985. “Monnaie, intérêt et dépenses publiques”, Economies et sociétés, n. 2, série MP (août).
- Graziani, Augusto. 1987. “Keynes’ Finance Motive”, Economies et Sociétés – Série Monnaie et Production, XXI, n. 9 : 23-42.
- Graziani, Augusto. 1994. “Real Wages and the Loans-Deposits Controversy”, Economie Appliquée, tome XLVl, n° 1, p. 31-46.
- Graziani, Augusto. 1996. “Money as Purchasing Power and Money as a Stock of Wealth in Keynesian Economic Thought”, In: Money in Motion: The Post Keynesian and Circulation Approaches, Ghislain Deleplace & Edward J. Nell ed. London: Macmillan Press Ltd & New York: St. Martin’s Press Inc.
- Graziani, Augusto. 2001. Teoria Economica, Macroeconomia. Quinta edizione riveduta e ampliata, Napoli: Edizioni Scientifiche Italiane.
- Graziani, Augusto. 2002. “New lines of research in monetary economics”, Ch.11 in Is There Progress in Economics? Knowledge, Truth and the History of Economic Thought, Stephan Boehm, Christian Gehrke, Heinz D. Kurz & Richard Sturn eds., pp.173-192, Cheltenham, UK: Edward Elgar.
- Graziani, Augusto. 2003a. The Monetary Theory of Production, Cambridge: Cambridge University Press.
- Graziani, Augusto. 2003b. “Microéconomie et macroéconomie : à qui la priorité ?”, Ch. 7 in Théories monétaires post keynésiennes, Pierre Piégay, Louis-Philippe Rochon ed., pp. 121-128 Paris: Economica.
- Graziani, Augusto. 2020. Mercato, Struttura, Conflitto: Scritti su economia italiana e Mezzogiorno. A cura di Adriano Giannola, Bologna: Il Mulino.
- Hendry, David. F. & Jean-François Richard. [1982] 1993. “On the formulation of empirical models in dynamic econometrics”, Journal of Econometrics, 20 (1982) 3-33, reprinted in Econometrics: Alchemy of Science, Oxford: Blackwell Publishers.
- Kalecki, Michal. 1942. “A Theory of Profits”, The Economic Journal, Vol. 52, No. 206/207 (Jun. – Sep.), pp. 258-267.
- Kalecki, Michal. [1954] 2010. Theory of Economic Dynamics: An Essay on Cyclical and Long-Run Changes in Capitalist Economy, London and New York: Routledge, originally London: Allen and Unwin.
- Lesourne, Jacques. 1977. A theory of the individual for economic analysis, Amsterdam & New York: North-Holland.
- Llorca, Matthieu Jean-Paul Guichard and Cingolani, Massimo. 2009. Évolutions des agrégats macro-financiers dans les Nouveaux Pays Membres et Candidats à l’UE, STAREBEI research report, 181 p.
- Malinvaud, Edmond. 1956. “L’agrégation dans les modèles économiques”, Cahiers du Séminaire d’Économétrie, No. 4 (1956), pp. 69-146.
- Messori, Marcello. 1998. “Agenti e mercati in uno schema periodale”, in Moneta e Produzione, a cura di Marcello Messori, 285-330, Torino: Giulio Einaudi Editore.
- Michell, Jo & Jan Toporowski. 2013-14. “Critical Observations on Financialization and the Financial Process”, International Journal of Political Economy, special issue on Understanding Financialization: History, Theory and Institutional Analysis, Vol. 42, No. 4 (Winter): pp. 67-82.
- Mockers, Jean-Pierre. 2016. Court traité d’économie et de politique économique : Bonne théorie : Bonne politique ; mauvaise théorie : … , Paris: L’Harmattan.
- Modigliani, Franco and Richard A. Cohn. 1979. “Inflation, Rational Valuation and the Market”, Financial Analysts Journal, 35, n. 2 (Mar. – Apr): pp. 24-44.
- Moore, Basil John. 1988. Horizontalists and Verticalists: The macroeconomics of credit money, Cambridge: Cambridge University Press.
- Parguez, Alain. 1996. “Beyond Scarcity: A Reappraisal of the Theory of the Monetary Circuit”, In: Money in motion: The Post-Keynesian and Circulation Approaches, Ghislain Deleplace & Edward Nell ed., London: Macmillan.
- Parguez, Alain & Mario Seccareccia. 2000. “The credit theory of money: the monetary circuit approach”, In: What is Money, John Smithin ed., pp. 101-123, New York and London: Routledge.
- Pasinetti, Luigi L. 1965. “Causalità e interdipendenza nell’analisi econometrica e nella teoria economica”, in: Annuario dell’Università Cattolica del S. Cuore, 1964-’65, 233-250, Bologna: Il Mulino.
- Pasinetti, Luigi. L. 1986. “Theory of value. A source of alternative paradigms in economic analysis”. In: Foundations of Economics: Structures of Inquiry and Economic Theory, Mauro Baranzini & Roberto Scazzieri eds., pp. 409–431. Basil Blackwell.
- Pasinetti, Luigi L. 1993. Structural economic dynamics: a theory of the economic consequences of human learning, Cambridge: Cambridge University Press.
- Pasinetti, Luigi L. & Nadia Garbellini. 2015. “From Sraffa: Backwards, To a Better Understanding of Marx’s Values/Prices “Transformation”; and Forward, To a Novel View of Growing Economic Systems”, Cahiers d’économie politique / Papers in Political Economy, n. 69, What have we learnt on Classical economics since Sraffa? / Qu’a-t-on appris sur l’économie classique depuis Sraffa?, pp. 73-96.
- Poulon, Fréderic. 2015. Economie générale, 8ème édition, Paris : Dunod.
- Roncaglia, Alessandro. 2024. Power and Inequality: A Reformist Perspective, Cambridge: Cambridge University Press.
- Salanti, Andrea. 1985. “Le assunzioni della teoria economica: Un’ipotesi interpretativa”. Note Economiche, 1985(1–2), 64–88
- Samuelson, Paul. 1958. “An Exact Consumption-Loan Model of Interest with or without the Social Contrivance of Money.”, Journal of Political Economy, 66, no. 6: 467–82.
- Schmitt, Bernard. 1966. Monnaie, salaires et profits, Paris : Presses Universitaires de France.
- Schmitt, Bernard. 1984. Inflation, chômage et malformations du capital, Paris & Albeuve : Economica & Castella.
- Schmitt, Bernard. 2012. “Relative prices are undermined by a mathematical error”, Ch. 1 in Modern Monetary Macroeconomics: A New Paradigm for Economic Policy, Claude Gnos & Sergio Rossi ed., 19-38, Cheltenham UK, Edward Elgar.
- Schneider, Erich. [1962] 2003. Money Income and Employment, London & New York: Routledge, 2003. Pubblicato originariamente a Londra da George Allen & Unwin Ltd, 1962.
- Seccareccia, Mario. 1982. “Keynes, Sraffa et l’économie classique : le problème de la mesure de la valeur”, L’Actualité économique, vol. 58, n° 1-2, 1982, p. 115-151, disponibile all’indirizzo : Seccareccia.
- Seccareccia, Mario. 2004. “Aspects of a New Conceptual Integration of Keynes’s Treatise on Money and the General Theory: Logical Time Units and Macroeconomic Price Formation”, In: Money Credit and the Role of the State, Essays in honour of Augusto Graziani, Neri Salvadori & Richard Arena ed., Aldershot: Ashgate.
- Schumpeter, Joseph A. [1911] 1949. The theory of economic development an inquiry into profits, capital, credit, interest, the business cycle, Cambridge, Massachusetts: Harvard University Press.
- Toporowski, Jan. 2000. The End of Finance: The theory of capital market inflation, financial derivatives and pension fund capitalism, London & New York: Routledge, (Routledge Frontiers of Political Economy, 25).
- Vallageas, Bernard. 1976. Le paradoxe du profit et le circuit économique. Essai sur la structure macroéconomique des sociétés capitalistes. Thèse présente pour le doctorat d’État es Sciences Économiques, Université de Dijon, Faculté de science économique et de gestion.
- Vallageas, Bernard 2010. “The circuit analysis, the monetary economy of production and the multisectorial analysis. Proposals for a S.N.A. built on income-value. A “detransformation” of prices in values.’. MPRA paper. https://mpra.ub.uni-muenchen.de/58916/1/MPRA_paper_58916.pdf.
- Vallageas, Bernard 2018. Monnaie, profit et valeur : un essai sur le circuit, l’économie monétaire de production et sur les liens entre la macroéconomie et l’analyse financière des entreprises. http://a.world.prod.model.free.fr/monnaie_profit_valeur.pdf.
Il circuito monetario di Augusto Graziani e la valutazione dell’impatto sociale delle operazioni bancarie
Massimo Cingolani1
La prima parte di questo contributo ricorda la definizione di moneta endogena data dal circuito monetario e accolta da Augusto Graziani, per poi descrivere quello che si potrebbe chiamare il “modello canonico” della versione del circuito da lui sviluppata, che fornisce una descrizione succinta del funzionamento di una macroeconomia che integra pienamente la moneta e le banche. La seconda accenna ad alcuni riscontri empirici del circuito monetario. Volgendo lo sguardo ai possibili sviluppi futuri, la terza parte presenta alcune idee sul possibile utilizzo della teoria del circuito monetario per la valutazione sociale delle operazioni bancarie.
1. Un po’ di teoria
1.1 Osservazioni generali
Le operazioni bancarie sono un tipo particolare di operazioni finanziarie, e come scrisse de Finetti nel 1935:
“Le operazioni finanziarie si riducono a scambi di denaro; a volerle considerare nella loro accezione più larga possibile, potremo anzi definire appunto le operazioni finanziarie come quei contratti di scambio in cui non figura nessuna merce fuorché il denaro”, De Finetti (1935, p. 471).2
Per valutare gli scopi di utilità collettiva dell’attività bancaria bisogna quindi ragionare su uno schema che integri pienamente la moneta e le banche e spieghi come queste si relazionano col resto del sistema economico e sociale. Il circuito monetario di Graziani soddisfa questi due requisiti e si differenzia in questo da molti approcci mainstream3. Come ricordato da Riccardo Bellofiore (2022), il circuito di Graziani è un modello economico a due beni (consumo e investimento) e a tre settori o poli istituzionali: le famiglie4, le banche e le imprese. In questo schema logico la moneta si definisce come una passività emessa del settore bancario, che viene utilizzata come mezzo di pagamento fra famiglie e imprese proprio perché estranea alle loro transazioni (definizione triangolare della moneta). Il ruolo specifico della banca in questo contesto è quello di produrre mezzi di pagamento emettendo una passività “liquida” creata contestualmente all’atto di consentire un credito, un attivo di bilancio che non è liquido, a differenza del passivo monetario corrispondente5.
1.1.1 La dimensione “sistemica” del circuito di Graziani
All’interno del sistema economico, l’attenzione di Graziani si focalizza sulle variabili monetarie a cui dedica un’analisi molto dettagliata, sviluppando di fatto il nocciolo di quello che si può indicare in gergo come il “blocco monetario e finanziario” di un modello macroeconomico6. In linea di principio, questa scelta rende possibile l’uso del circuito monetario in modelli con interpretazioni economiche diverse, perché il blocco di equazioni che spiega le variabili monetarie può essere integrato in schemi che possono spaziare, al limite, dai modelli neoclassici di breve termine ai modelli di lungo termine alla Garegnani o alla Pasinetti7.
Ma pur concentrandosi sul fenomeno monetario, l’analisi non perde di vista l’aspetto sistemico. Post-Keynesiani come Eichner (1991) o Mockers (2016), ma anche molta dell’economia classica e neoclassica e in particolare i modelli di Leontief, hanno recepito l’idea di applicare la teoria dei sistemi all’economia, e si può senz’altro dire di Graziani che, pur sviluppando principalmente il blocco monetario, ragiona in una logica macroeconomica di sistema. Di fatto, una delle sue conclusioni più keynesiane, ripetuta in vari scritti, è che, proprio a causa dell’integrazione della moneta, si crea un effetto sistemico per cui il tutto non è più la somma delle parti8. La moneta è cioè un elemento che spiega la “fallacia della composizione” messa in luce dall’analisi keynesiana9. Può essere utile ricordare a riguardo che la letteratura francese, che Graziani conosceva molto bene, ha da tempo identificato il carattere sistemico del circuito e in particolare Poulon (2015, pp. 9-94), uno dei fondatori del circuito, va fino ad opporre il “paradigma sistemico” del circuito a quello “insiemistico” dell’equilibrio generale10.
1.1.2 Caratteristiche della moneta circuitista
Nel circuito di Augusto Graziani la moneta ha alcune caratteristiche importanti ed è utile ricordarne cinque.
1.1.2.1 Sequenzialità: Si tratta in primo luogo di una moneta inserita in una dinamica temporale all’interno della quale la sua definizione è triangolare (cf. §1.1.2.5), e quest’analisi dinamica è un’analisi sequenziale nel tempo storico. In questo, il circuito di Graziani è diverso dal circuito di Schmitt (1984), che si svolge nel cosiddetto tempo quantico, ed è molto vicino e simile a quello di Alain Parguez (1996 e, con Seccareccia, 2000). Una delle conseguenze di questa sequenzialità è che esiste una causalità che è per lo più esclusa dai modelli simultanei e che in linea di principio è possibile solo nei modelli sequenziali. A rigore la possibile causalità dovrebbe essere una premessa logica per discutere l’effetto di uno strumento di politica economica (variabile che si vorrebbe idealmente esogena) su una variabile obiettivo (che dovrebbe essere endogena) 11.
1.1.2.2 Focalizzazione sul singolo periodo: In questa dinamica, Graziani si concentra su un periodo singolo che analizza e scompone nelle sue fasi, che sono anch’esse sequenziali, e in queste fasi la moneta si trasforma prima in reddito e poi in consumo e risparmio. Questa scomposizione illustra la duplice natura di flusso e di stock della moneta (Graziani, 1996 e 2002). Al termine del singolo periodo, ci può essere sia la situazione di equilibrio che è descritta nell’articolo del 1984, Moneta Senza Crisi (Graziani 1984b), o quella “di crisi” che è descritta nell’introduzione al libro del 1980 della Costabile su Malthus12. La differenza che corre fra le due è che nel primo caso la moneta creata all’inizio del circuito è interamente distrutta al suo termine, mentre nel secondo non lo è. In entrambi i casi, finito il periodo “singolo”, seguono altri periodi; quindi, a seconda che il primo periodo sia finito in equilibrio o in crisi, il periodo successivo comincia “in equilibrio” o in crisi e in tal caso può generare più facilmente una dinamica “dello squilibrio”13.
1.1.2.3 Legame con la distribuzione dei redditi: Nel circuito c’è anche un legame con la distribuzione dei redditi, perché la moneta viene creata come reddito. Come per gli economisti classici, la distribuzione del reddito coinvolge le classi sociali; quindi, c’è in Graziani un rifiuto radicale dell’individualismo metodologico, che è la ragione fondamentale della sua critica all’approccio mainstream14. Una delle conseguenze indirette di quest’impostazione macroeconomica alla distribuzione è che, consolidando i profitti a livello di imprese, quindi di classe capitalistica, questi si annullano e il profitto si rivela essere un mero trasferimento.
1.1.2.4 Causalità dell’investimento sul risparmio: Va sottolineato anche che il circuito recepisce l’ipotesi classica che il salario è pagato in anticipo (Graziani, 1994); quindi, c’è un “fondo salario” che nei fisiocratici e negli economisti classici era il grano accumulato nel periodo precedente, ma che diventa invece con Schumpeter e i circuitisti che in questo lo hanno seguito, una creazione di potere d’acquisto monetario fatta dalle banche ex novo, che ribalta la causalità fra risparmi e investimenti. Se in una società agricola bisognava accumulare prima un risparmio reale (il grano) per poter pagare i salari in anticipo, nella società industriale retta da un’economia monetaria questo non è più necessario. Con la creazione monetaria è la spesa che crea il risparmio, aspetto Keynesiano per eccellenza, che è anche il punto di partenza della teoria dei profitti di Kalecki (1942)15. La causalità tra investimenti e risparmio corrisponde dunque logicamente alla causalità dei prestiti sui depositi.
1.1.2.5 Scorporo delle banche dal resto del settore produttivo privato: Infine, un altro contributo logico fondamentale del circuito su cui insiste molto Graziani è la separazione in due del settore privato tra settore bancario che produce moneta, e settore non-bancario che la usa16. Senza separazione fra banche e imprese è difficile integrare la moneta in un modello macroeconomico e questo problema riguarda sia l’analisi neoclassica che quella neokeynesiana (incluso Patinkin). Graziani ricorda infatti che, qualsiasi sia la ragione per cui alla fine si detengono delle scorte liquide (pagamento o transazione), il riflusso completo che avviene alla chiusura del circuito nel caso senza crisi (distruzione totale delle liquidità create nell’efflusso iniziale che finanzia la produzione), corrisponde a una variazione nulla di tali scorte, condizione sulla quale Graziani costruisce un’ipotesi di equilibrio monetario nel circuito. Al contrario, la costanza delle scorte liquide rimane implicita in qualsiasi trattazione macroeconomica classica o neoclassica che, prendendo come periodo di riferimento un lasso di tempo di durata superiore a quello entro il quale la moneta nasce muore e scompare, fa astrazione della moneta stessa. In tal caso si escludono ab initio le variazioni delle scorte monetarie, trasformando così la loro nullità, che Graziani presenta come una possibile condizione di equilibrio, in un’identità17.
Senza questa disaggregazione del settore privato rispetto alla produzione e all’uso della moneta non ci può essere moneta triangolare, cioè moneta nel senso circuitista18, la quale è normativamente una moneta “senza signoraggio”. Quando esiste, cioè fuori dall’equilibrio a liquidità invariata, questo signoraggio può essere solo “privato”, poiché non c’è settore pubblico nel modello canonico di Graziani. Come ha giustamente osservato Riccardo Bellofiore in diverse occasioni, questo è uno dei pochi punti in cui il circuito di Graziani differisce da quello di Parguez.[18]
1.2 Il modello canonico del circuito monetario di Graziani
1.2.1 Presentazione del modello
Fatte queste considerazioni generali, si può presentare un modello che si può definire “canonico” del circuito monetario di Graziani e che, come osservato precedentemente, esclude sia il settore pubblico che il settore estero. Queste ed altre ipotesi semplificatrici (la cui scelta è brillante a giudizio di chi scrive) permettono a Graziani di mettere a fuoco gli elementi pregnanti del problema dell’integrazione della moneta. Infatti, nel modello così semplificato le famiglie possono risparmiare solo in contante o in titoli emessi dalle imprese e quindi l’allocazione del risparmio si fa all’interno del solo settore privato fra passività bancarie liquide e passività delle imprese a più lunga scadenza. La semplificazione chiarisce anche perché la moneta triangolare necessita la scissione del settore produttivo privato in banche e imprese produttrici di beni.
Nella fase di efflusso, le imprese chiedono alle banche di creare liquidità monetaria per un valore equivalente ai salari da distribuire, che utilizzano per pagare il lavoro occorrente per la produzione di beni di consumo e di beni d’investimento. Le famiglie, che sono il terzo apice del triangolo produttivo dell’economia monetaria di produzione, vengono pagate coi salari, che diventano così creazione monetaria di valore, cioè reddito, prima di trasformarsi in consumo e risparmio. Come nello schema della riproduzione marxiana ripreso anche da Kalecki (1942), il fatto che il monte salari possa essere speso solo per l’acquisto di beni di consumo, implica logicamente che questi ultimi siano acquistati e venduti a un prezzo superiore al loro costo di produzione.
Cosa succede all’interno del periodo singolo del circuito? I capitoli IV a VI del testo del 2003 sulla Teoria Monetaria della Produzione danno una risposta in 14 equazioni che sono esposte nel riquadro che segue[19]. In questa versione del “blocco macro-monetario e finanziario” di Graziani, ci sono 9 variabili esogene, cioè quelle che sono considerate come date durante il periodo, e 14 variabili endogene determinate da 14 relazioni. La maggior parte delle variabili esogene, sono decise dalle imprese e dalle banche. Tra queste, le variabili cruciali sono il livello totale dell’impiego N, il tasso reale di investimento b, definiti dalle imprese, e il salario w e la produttività π che, essendo dati, presuppongono implicitamente un orizzonte di breve periodo, che intuitivamente si può far coincidere col ciclo annuale della produzione.
Scegliendo un livello dato di occupazione N, le imprese fissano anche il livello della produzione reale e, definendo la quota del prodotto destinata all’investimento reale b, decidono anche la proporzione di lavoratori che destinano alla produzione di beni di consumo piuttosto che a quella di beni di investimento. Nel circuito le decisioni delle famiglie sono quindi subordinate a quelle delle imprese, poiché queste ultime, come illustrato nello schema di Graziani, decidono sia il livello della produzione (via N), che quello della distribuzione (via b), e attraverso quest’ultimo il livello dei prezzi (p) [20].
Come si vede dalla prima relazione, la ripartizione del prodotto (o del lavoro, dato che anche la produttività è data) fra consumo e investimenti, determina il livello dei prezzi, che risulta uguale al prodotto di un margine di profitto, dato dal rapporto tra la propensione al consumo e uno meno la propensione all’investimento reale, moltiplicato per un termine di costo unitario, dato dalla somma del costo del lavoro e del costo dell’interesse per unità di prodotto. Questa relazione di prezzo è centrale perché determina la distribuzione dei redditi che, come osserva Graziani, il circuito riprende da Kalecki (1942)[21].
Figura 1:Blocco macro-monetario e finanziario nel modello canonico del circuito di Graziani

È opportuno soffermarsi sul significato del margine di profitto nella dinamica temporale che intercorre fra finanza iniziale e finanza finale nel circuito di Graziani, che, va ricordato, si fonda sulla sua lettura del finance motive di Keynes (Graziani, 1984c e 1987)[22]. Mario Seccareccia (2004) ha sottolineato le origini wickselliane del circuito di Graziani in un suo notevole contributo a un volume in onore di Graziani che contiene anche diverse altre analisi circuitiste di grande interesse. Le idee di Wicksell, per cui si rimanda anche a Bellofiore (1998), hanno influenzato “equilibristi generali” come Hayeck e Lindbeck, ma anche il Keynes del Trattato sulla Moneta che, come dimostra Seccareccia e come ha sostenuto anche Graziani (1981), è sostanzialmente coerente col Keynes della Teoria Generale. Seccareccia ha inoltre sollevato a diverse riprese un’interessante obiezione sul markup fisso che appare nella relazione di prezzo (1) che Graziani deriva dall’uguaglianza fra domanda e offerta globale. Secondo lui, in un modello propriamente post-keynesiano, il markup dovrebbe essere variabile e non fisso (Eichner, 1973) e, soprattutto, non dovrebbe derivare da un’eguaglianza “walrasiana” fra domanda e offerta globale. Se quest’obiezione ha molti meriti, non inficia però il fatto già rilevato che nel circuito, come nell’analisi di Sraffa, sono le imprese a decidere e non i consumatori. Infatti, una volta concordato il valore monetario iniziale della produzione con le banche, le imprese fissano anche le altre variabili della produzione e della distribuzione ad eccezione del risparmio delle famiglie e della frazione di quest’ultimo detenuta sotto forma liquida. È peraltro solo il risparmio liquido delle famiglie che rappresenta per loro un problema, perché genera un uguale indebitamento addizionale nei confronti del settore bancario, che è a sua volta per loro una perdita di reddito reale. Le imprese sono invece indifferenti al risparmio delle famiglie sotto forma di titoli, poiché, dato che controllano sia i prezzi che la distribuzione, possono ripercuotere su di loro l’intero costo degli interessi sui titoli, fissando il tasso di interesse sulle obbligazioni a un valore sufficientemente alto per compensare quello che le banche offrono sui depositi. Viceversa, per quanto riguarda le loro relazioni con le banche, le imprese sono costrette a prelevare il pagamento degli interessi sui propri profitti e ciò comporta per loro una perdita di reddito reale, come si evince dalla relazione (9). Questo sottolinea un aspetto essenziale del circuito che è che all’interno del periodo di produzione, che è anche quello della creazione-distruzione totale di moneta nel caso senza crisi, avviene una redistribuzione del valore-salario iniziale della produzione finanziato dalla moneta credito fra quella che poi diventa al momento della finanza finale la ripartizione fra salari, profitti e interessi[23]. Inoltre, se è vero che nel periodo compreso fra la finanza iniziale e la finanza finale le imprese determinano un markup che è effettivamente fisso, dato che questo periodo è di durata arbitraria, si può fare tendere a zero, permettendo al limite un aggiustamento continuo del markup e quindi, in sostanza, una sua variabilità temporale. Al di là di quest’aspetto meramente formale, il punto di sostanza resta che nel modello di Graziani sono le imprese a fissare sia il livello che la composizione del prodotto e dell’occupazione e, dato che quest’ultima fissa il markup, hanno in mano tutte le leve della decisione. Il fatto che il livello del markup si deduca eguagliando domanda e offerta globale, anche se compatibile con Hayeck o Walras, è soprattutto un’applicazione del concetto di domanda effettiva di Keynes[24].
Di fatto, generalizzando su basi Kaleckiane l’ipotesi di mercati competitivi accolta da Keynes, nel modello di Graziani le imprese possono fissare i prezzi su basi oligopolistiche e disporre in pratica della stessa capacità di determinare prezzi e quantità di quella che avrebbero in caso di monopolio puro.
Come sottolinea Graziani (2003, pp. 103-104) è chiaro dalle relazioni (7)-(9) sui profitti, che: (i) il tasso di profitto può, come in Kalecki, essere positivo, solo quando le imprese investono più di quanto le famiglie non risparmiano (b>s); (ii) i profitti monetari dipendono direttamente dal livello dei prezzi e aumentano con il tasso di interesse che le imprese pagano alle famiglie sui titoli iB, che è a sua volta funzione di iL e iD; e iii) i profitti reali non dipendono dal tasso di interesse iB che le imprese pagano sui titoli che vendono alle famiglie, ma, attraverso l’aumento dei prezzi, si riducono in funzione del tasso di interesse pagato alle banche iL che è un trasferimento di reddito reale. Quando la propensione all’investimento e la propensione al risparmio coincidono (b=s), i (sovra-)profitti si annullano e ci si trova nel caso della concorrenza perfetta. Nel caso di risparmio delle famiglie nullo (s=0), “i capitalisti guadagnano quello che spendono mentre i lavoratori spendono ciò che guadagnano”[25].
Le relazioni (10) – (14) illustrano la formazione dei tassi di interesse in base all’eguaglianza fra domanda e offerta di risparmio al momento di chiusura del circuito. La relazione (10)[26] traduce quest’eguaglianza sotto un’ipotesi ragionevole sulla specificazione dell’offerta e della domanda di titoli[27] e, una volta verificata, consente alla (12) di determinare sia la domanda che l’offerta di risparmio. La (10) implica che, perché si abbia eguaglianza fra offerta e domanda di risparmio, una volta fissato il tasso di interesse iD pagato dalle banche sulle scorte liquide, il tasso di interesse iB sui titoli emessi dalle imprese si determina come funzione lineare di iL quando a e b sono dati, livello che non corrisponderà necessariamente alla piena occupazione. Se, oltre a questo, si ammette che tutto il risparmio delle famiglie è investito in titoli emessi dalle imprese (bd=1), si ha anche una variazione nulla delle scorte liquide che può essere considerata in prima approssimazione una condizione per l’equilibrio finanziario delle imprese (Graziani, 2003, p. 125)[28].
Le 14 variabili endogene: B, C, iB, Im, Ir, p, r, P, Pr, X, Y, ΔL, dD, S, sono determinate dalle relazioni (1)-(14) e dalle variabili esogene, come riassunto nel riquadro che segue. Le esogene[29] comprendono due variabili macroeconomiche “strutturali”: la produttività p e il salario w. Oltre a queste, ci sono sette variabili di decisione, delle quali due sono determinate dalle famiglie: il tasso di risparmio s e la preferenza per la liquidità b. Le altre sono determinate dalle imprese: l’impiego totale N, la propensione reale all’investimento b e il coefficiente di preferenza per il credito delle imprese m; o dalle banche: il tasso di interesse pagato dalle imprese sui prestiti iL e il tasso di interesse pagato dalle banche sui depositi iD.
Figura 2: Lista delle variabili esogene e endogene del modello
 1.2.2 Alcune simulazioni numeriche
1.2.2 Alcune simulazioni numeriche
Per illustrare il comportamento del modello di Graziani durante il periodo singolo a cui fa riferimento, si presentano alcune simulazioni dando dei valori virtuali alle variabili e ai parametri esogeni che determinano una soluzione centrale che viene poi confrontata con quella ottenuta modificando una sola delle esogene alla volta. Questa seconda soluzione corrisponde a una “derivata parziale” del sistema rispetto a un cambiamento di una sola delle esogene in prossimità della soluzione centrale. Tale sensibilità illustra la meccanica del modello (che è diversa da quella del modello neoclassico). Non pretende fornire una descrizione realistica di cosa accadrebbe se nella realtà la variabile esogena si modificasse come indicato. Lo scopo non è infatti l’uso del modello per la formulazione di proiezioni o scenari, ma la comprensione delle sue proprietà. In simulazioni realistiche altre esogene si muoverebbero insieme all’esogena considerata e quindi eventuali scenari alternativi dovrebbero calcolare l’effetto del cambiamento di varie esogene contemporaneamente.
1.2.2.1 Simulazione di riferimento: Se si danno i valori seguenti alle variabili e ai parametri esogeni si ottengono i valori riportati nel riquadro di destra per le variabili endogene[30]:
Figura 3: Valore delle esogene e delle endogene nella soluzione di riferimento 1.2.2.2 Variazione esogena di N: Partendo da questa soluzione di riferimento, se si fa variare l’occupazione totale da 700 a 1400 si può vedere nelle tre simulazioni descritte nei grafici che seguono che le variabili distributive (S, P, Im, B, L aumentano proporzionalmente mentre i principali parametri finanziari (bd, iB, r) e in particolare il tasso di profitto restano immutati. Il grafico non è riprodotto, ma anche i prezzi restano immutati, mentre, nella logica Keynesiana del circuito sia il consumo che il reddito reale delle famiglie aumentano immediatamente per effetto dell’aumento dell’attività.
1.2.2.2 Variazione esogena di N: Partendo da questa soluzione di riferimento, se si fa variare l’occupazione totale da 700 a 1400 si può vedere nelle tre simulazioni descritte nei grafici che seguono che le variabili distributive (S, P, Im, B, L aumentano proporzionalmente mentre i principali parametri finanziari (bd, iB, r) e in particolare il tasso di profitto restano immutati. Il grafico non è riprodotto, ma anche i prezzi restano immutati, mentre, nella logica Keynesiana del circuito sia il consumo che il reddito reale delle famiglie aumentano immediatamente per effetto dell’aumento dell’attività.
Grafico 1: Sensibilità a una variazione del livello di occupazione N deciso dalle imprese [700-1400]

1.2.2.3 Variazione esogena di b: La simulazione successiva è relativa a una variazione del tasso di investimento reale b fra 0.2 e 0.5 e illustra che gli effetti di questa variazione passano principalmente attraverso il tasso di profitto reale e i prezzi, che aumentano fortemente.
Controllando i prezzi, le imprese, che privilegiano l’autofinanziamento, li aumentano e così aumentano sia i profitti nominali che l’investimento in valore monetario. Al contrario sia il consumo reale che il reddito reale delle famiglie si contraggono a causa dell’aumento dei prezzi, poiché in questa variante non ci sono né aumenti salariali, né l’aumento della produttività che in uno scenario realistico sarebbero contestuali a un aumento degli investimenti. Questo conferma però che la meccanica del modello consente alle imprese di finanziare un aumento degli investimenti attraverso una diminuzione del reddito e del consumo reale delle famiglie. Dal punto di vista della politica economica non basta quindi creare le condizioni per aumentare i profitti e gli investimenti, ma bisogna anche aumentare i salari e la produttività perché aumenti il benessere collettivo. In conclusione, attraverso b si modifica il livello dei prezzi, il tasso di investimento, il tasso di profitto e quindi il tasso di autofinanziamento.
Grafico 2: Sensibilità a una variazione del tasso di investimento b [0.2-0.5]

1.2.2.4 Variazione esogena di s: Facendo variare il tasso di risparmio delle famiglie s tra il 5% e il 25% si osserva che risparmio, titoli detenuti e liquidità aumentano, mentre i profitti diminuiscono e gli investimenti nominali restano costanti.
Grafico 3: Sensibilità a una variazione del tasso di risparmio s [5%-25%]

Scende anche il tasso di profitto reale per effetto dell’aumento dei prezzi. Alla fine, mentre il consumo nominale e quello reale restano pressoché costanti, il reddito reale aumenta per effetto dell’aumento del risparmio che gonfia la ricchezza detenuta in titoli e, dato il contestuale aumento della liquidità, determina un maggiore indebitamento delle imprese presso le banche.
1.2.2.5 Variazione esogena di p: Facendo variare la produttività π tra 1.1 e 1.5 l’effetto meccanico si ha sui prezzi, che diminuiscono facendo aumentare il consumo e il reddito reale. Viceversa, le variabili nominali e monetarie restano costanti.
Grafico 4: Sensibilità a una variazione del tasso di produttività p [1.1-1.5]

1.2.2.6 Variazione esogena di w: Facendo variare il salario nominale w tra 8 e 12 il primo effetto si fa sentire sui prezzi, che aumentano fortemente.
Grafico 5: Sensibilità a una variazione del salario w [8-12]

Tutte le variabili nominali di conseguenza crescono, mentre i parametri finanziari restano costanti, come anche il consumo e il reddito reale delle famiglie, i cui grafici non sono riprodotti.
1.2.2.7 Variazione esogena di μ: Se si esamina l’effetto di una variazione del coefficiente di preferenza delle imprese per il credito bancario m facendolo variare fra 0.13 e 0.33 si vede che le imprese prendono più prestiti a scapito delle obbligazioni B che emettono presso le famiglie. Dato che i tassi di interesse sui prestiti si presumono costanti, l’aumento dell’indebitamento riduce i profitti nominali e gli investimenti. Tuttavia, il tasso di profitto resta costante, mentre diminuiscono sia il tasso di interesse sulle obbligazioni che la quota di risparmio che le famiglie detengono sotto forma di titoli. La riduzione del tasso di interesse sul debito delle imprese verso le famiglie provoca una riduzione dei prezzi, che spiega la riduzione nominale delle variabili nominali (consumo, investimento e risparmi). Il consumo e gli investimenti diminuiscono in termini nominali, ma in termini reali sia il consumo che il reddito restano costanti (grafico non riprodotto).
Grafico 6: Sensibilità alla variazione del coeff. di preferenza delle imprese per il credito bancario m [13%-33%]

1.2.2.8 Variazione esogena di β: Facendo variare il coefficiente di liquidità delle famiglie b fra 0.25 e 0.45, anche qui lasciando costanti sia il tasso di interesse sui depositi iD e quello sui prestiti iL, il tasso di interesse consentito dalle imprese sui loro titoli iB aumenta, e aumenta ancora più rapidamente la domanda di titoli, mentre non muta il tasso di profitto. I prezzi rimangono costanti, cosi come i profitti nominali, il risparmio e gli investimenti, mentre il risparmio investito in titoli aumenta a scapito dei maggiori prestiti che le imprese prendono dalle banche. Il consumo e il reddito reale non mutano, né cambiano i loro livelli nominali.
Grafico 7: Sensibilità a una variazione del coefficiente di liquidità delle famiglie β [0.01-0.2]

1.2.2.9 Variazione esogena di iL: Infine si considera l’aumento del tasso di interesse sui prestiti alle imprese iL dall’uno al cinque percento.
Grafico 8: Sensibilità a una variazione del tasso di interessi sui prestiti delle banche alle imprese iL [1.0-1.05]

Si vede sui grafici precedenti che, dato che si suppone la costanza degli altri parametri monetari esogeni (propensioni alla liquidità delle imprese e delle famiglie), il principale effetto di un aumento di un tasso di interesse sui prestiti alle imprese è quello di aumentare il tasso di interesse che le imprese offrono sulle proprie obbligazioni. Così facendo, le imprese compensano la riduzione dell’indebitamento verso le banche (ΔL) che è provocata dal maggior costo dell’interesse, con l’aumento del debito delle imprese verso le famiglie. Tramite l’equazione dei prezzi, le imprese neutralizzano ogni effetto reale cosicché non cambiano sostanzialmente né il risparmio delle famiglie, né i profitti, né gli investimenti monetari. Non ci sono quindi neanche effetti reali sul consumo e sul reddito delle famiglie perché i loro valori nominali sono aggiustati all’inflazione.
1.3 La chiusura del circuito e la doppia condizione di equilibrio reale e finanziaria
Al termine del capitolo VI, Graziani (2003) osserva che nel circuito ci sono due condizioni di equilibrio che determinano il livello di disoccupazione e che investono le variabili monetarie del modello e i tassi di interesse.
Per vederlo, si può partire dalla relazione (10) che determina il tasso di interesse sui titoli emessi dalle imprese iB che congiuntamente con (12) permette loro di recuperare la proporzione bd della domanda di risparmio che risulta dalle preferenze per la liquidità dei consumatori (β), quelle per il credito delle imprese (μ) e dai tassi di interesse sui depositi iD e quelli sui prestiti alle imprese iL. Come già osservato, se sono dati i coefficienti di comportamento b e m e il tasso di interesse pagato dalle banche sui depositi iD, la (10) esprime una relazione lineare fra il tasso di interesse sui prestiti che le banche consentono alle imprese e il tasso che le imprese offrono ai risparmiatori sui titoli che emettono. La figura 4 qui sotto[31] illustra questa relazione che è una retta nel piano cartesiano di ascissa iL e di ordinata iB. Supponendo che la situazione iniziale rifletta condizioni di piena occupazione e quindi la retta di inclinazione β1 (linea blu) corrisponda all’equilibrio del mercato dei capitali con piena occupazione, ponendo la condizione aggiuntiva bd=1, si può calcolare il valore della coppia (iB,iL) tale per cui tutto il risparmio delle famiglie sarà investito in titoli, situazione che può essere interpretata come un equilibrio monetario dinamico per le imprese, perché corrisponde alla costanza delle scorte liquide detenute dalle famiglie, e quindi a una quantità di moneta invariata, ipotesi che, come osserva Graziani, sono anche quelle accolte da Keynes nella Teoria Generale.
.
Figura 4: Dinamica della variazione della preferenza per la liquidità

Con i parametri considerati nella figura 4, questo felice connubio si realizza al punto C quando le banche fissano il tasso di interesse iL sui prestiti all’8.16%. In tal caso, le imprese fisseranno il tasso che pagano sui titoli detenuti dalle famiglie a iB=11.4%. Questo punto C nel grafico a sinistra, corrisponde alla piena occupazione (per ipotesi) e alla costanza delle scorte liquide (per il valore particolare scelto per la coppia dei tassi di interesse), una combinazione di eventi che logicamente dovrebbe incitare le imprese a mantenere la piena occupazione nel periodo successivo. Se però durante il periodo di produzione il coefficiente di preferenza per la liquidità cambia, ed aumenta ad esempio da β1 a β2, la retta che dà gli equilibri del mercato dei capitali ruota verso l’alto (linea arancio) e non coinciderà più col pieno impiego. Se allora le banche lasciano invariato il loro tasso sui prestiti iL all’8.16%, il nuovo tasso sui titoli si assesterà al 16.7% (punto C’), e questo aumento sarà accompagnato da una riduzione del coefficiente di preferenza per i titoli bd, dei titoli stessi B e da un aumento della liquidità ΔL e dei prestiti. È quindi plausibile che all’inizio del periodo successivo le imprese cha hanno subito un trasferimento reale di reddito verso le banche saranno portate a ridurre la produzione e l’impiego.
Il circuito mostra quindi che ci sono due condizioni di piena occupazione delle quali l’economia Keynesiana tradizionale considera solo la prima: i) il tasso di interesse e il livello dell’investimento devono permettere la piena occupazione, come usualmente richiedono i modelli Keynesiani; ii) ci dev’essere un equilibrio finanziario fra banche e imprese la cui mancata realizzazione può essere causa di disoccupazione, fatto che non può essere esplicitato se non si scinde in due il settore privato isolando le banche (Graziani, 2003 p. 128)[32]. Questo spiega perché la piena occupazione è estremamente instabile dal punto di vista della successione dinamica dei singoli periodi. La dinamica prefigurata da Graziani è, come in Kalecki, quella di una successione di squilibri di breve periodo. Prevale quindi il caso “malthusiano” di chiusura del circuito “con crisi”.
2. Cenni sulla pertinenza empirica del circuito
In questa sezione si riportano i risultati di lavori svolti in passato finora non pubblicati e si presentano dati più recenti sull’evoluzione di alcuni aggregati macro-finanziari relativi a verifiche empiriche del circuito.
2.1 Uno studio del 2008
Nel 2008 l’Istituto Bei finanziò uno studio svolto presso l’università di Nizza nel quale la teoria del circuito monetario fu sottoposta a test empirici fatti sui paesi di Visegrad (Repubblica Ceca, Repubblica Slovacca, Slovenia e Ungheria) e la Turchia con gli strumenti econometrici in voga all’epoca. La ricerca confermò la validità del circuito monetario. Cinque ipotesi furono sottoposte a stima econometrica per i paesi Visegrad e i risultati sono riassunti nel riquadro che segue.
Figura 5: Sintesi dello studio Starebei del 2008

Su base di quest’esperienza si può dire che una delle difficoltà dei test empirici sul circuito monetario è che non si osserva la finanza iniziale (si veda anche la sezione 2.3). Sotto certi aspetti si potrebbe dire che la finanza iniziale è la somma dei salari, sotto altri aspetti si può dire che è il PIL, cioè (circa) la somma dei redditi da lavoro e da capitale, anche se entrambi gli aggregati in contabilità nazionale sono osservati a chiusura dell’esercizio e hanno quindi a che fare con la finanza finale. In realtà non c’è una variabile osservabile che corrisponde esattamente al concetto di finanza iniziale. Occorrerebbe quindi integrare meglio nelle stime quello che si chiama il processo generatore dei dati (Hendry & Richard [1983] 1993), cosa che non è sempre facile.
2.2 La creazione di moneta e la dinamica dei salari e della ricchezza finanziaria[33]
Per definizione, non essendo neutra rispetto alla formazione del valore, la moneta circuitista può incidere sui prezzi relativi. In particolare, l’eventuale finanziamento monetario della speculazione può favorire la crescita più rapida del valore di mercato delle attività finanziarie relative al circuito del risparmio accumulato, piuttosto che quello delle attività legate alla generazione dei redditi correnti e in particolare i salari. Il circuito può così illustrare e spiegare la finanziarizzazione, che, anche se è un concetto discutibile che andrebbe precisato (Toporowski & Mitchell, 2013&14), resta uno dei fenomeni macro-finanziari più macroscopici degli ultimi decenni.
Infatti, una volta accettata la definizione di moneta come passività “terza” emessa dalle banche per fare i pagamenti, si capisce anche che la moneta deposito che viene creata al momento del prestito e viene distrutta quando il prestito è rimborsato può essere prestata nel frattempo per finanziare l’acquisto di titoli reali e finanziari e quindi influenzare il loro prezzo. Inoltre, esulando dal quadro semplificato del modello canonico del circuito, all’interno del periodo di produzione, la moneta può anche essere creata dalle banche per l’acquisto di titoli, e quindi potenzialmente svolgere un ruolo speculativo[34].
I grafici che seguono illustrano le evoluzioni divergenti dei prezzi relativi delle attività finanziari e dei flussi legati alla creazione del reddito, la cosiddetta inflazione del prezzo degli attivi (Toporowski, 2000), e possono essere interpretati in chiave circuitista.
Grafico 9: Salari, interesse e attivi finanziari USA 1954-2016

Se prendiamo ad esempio il caso degli Stati Uniti nel Grafico 9, comparando l’evoluzione a lungo termine di un paniere di beni salariali e di un paniere di beni finanziari si osserva che l’indice salariale ha perso terreno permanentemente rispetto a quello finanziario. Se un lavoratore avesse avuto 3 $ nel 1957[35] e li avesse investiti in un indice che fosse progredito allo stesso ritmo del valore dei salari nell’industria manifatturiera americana (linea marrone), nel 2016 avrebbe avuto 32 $. Se invece l’avesse investito in un indice che si fosse comportato come quello delle obbligazioni a lungo termine americane, nel 2016 avrebbe disposto di un capitale di 100 $ (linea blu). La cesura fra le curve blu e marrone avviene nel 1979-1980, anni a partire dai quali divergono, come confermato dall’evoluzione della linea verde, che illustra la differenza accumulata fra di esse e che diventa positiva a partire dal 1982. Le colonne in giallo rappresentano invece l’evoluzione del rapporto tra attività finanziarie e PIL negli Stati Uniti, che è passato da un valore inferiore a due fino agli anni Ottanta a un valore di circa cinque nel 2016. La finanziarizzazione si manifesta quindi nella forma di un aumento del valore degli stock finanziari rispetto ai flussi produttivi che riflette un’evoluzione negativa del prezzo relativo del lavoro. Lo stesso tipo di evoluzione si può osservare nel grafico che segue per il Regno Unito, con delle fasi temporali che sono però diverse.
Grafico 10: Salari, interesse e attivi finanziari UK 1960-2016

Se si prende un indice pari a una sterlina nel 1963 che avesse progredito come i salari orari nel settore manifatturiero inglese (linea marrone), nel 2016 questo avrebbe raggiunto un valore nominale di 46 UKP. La stessa sterlina del 1963, investita invece in un indice che fosse aumentato come il tasso a lungo termine sulle obbligazioni di Stato inglesi (linea blu nel grafico), sarebbe arrivata a valere 54 UKP nel 2016. La divergenza accumulata fra i due indici è rimasta negativa (cioè favorevole ai salari) tra il 1970 e il 1996 e ha toccato il suo minimo nel 1982, anno a partire dal quale ha cominciato a recuperare per diventare positiva nel 1996 e raggiungere il valore di circa 16 nel 2016. Per il periodo in cui i dati sono disponibili, che comincia nel 1979 il rapporto tra attività finanziarie e PIL che era di 1.85 nel 1979 è aumentato a 3.6 nel 1991, per salire a 15.1 nel 2008 ed è poi sceso a 11.7 nel 2016.
Grafico 11: Salari, interesse e attivi finanziari EZ 1973-2016

Infine, anche per quanto riguarda la zona Euro, i dati indicano che un Euro del 1973, investito in un indice che fosse cresciuto come i salari orari nel settore manifatturiero (linea marrone), nel 2016 avrebbe raggiunto il valore nominale di 11 Euro. Lo stesso Euro, investito in obbligazioni a lungo termine, avrebbe raggiunto un valore nominale di 20 Euro nel 2016 (linea blu). La divergenza accumulata fra i due indici è rimasta in territorio negativo dal 1973 al 1986 per poi eccedere 10% nel 1989 e raggiungere 48% nel 2016. Il rapporto tra attività finanziarie e PIL che era di 4.83 nel 1999, è salito a 6.88 nel 2016.
L’evoluzione sfavorevole del prezzo relativo del lavoro rispetto a quello di attività finanziarie come le obbligazioni a lungo termine documentata nei grafici precedenti è confermata quando si esaminano altre forme di destinazione del risparmio come fatto nel grafico 12 qui di seguito che esamina l’evoluzione dei prezzi relativi di varie attività finanziarie e reali confrontando il valore nominale di queste attività nel 2015 a quello che avevano nel 1995[36]. Si vede sul grafico che il valore del totale delle attività finanziarie è stato moltiplicato per 5.4, mentre quello dell’indice dei prezzi residenziali è stato moltiplicato per 3.5, quello degli attivi fissi (investimento reale) per 2.6, quello delle obbligazioni a lungo termine per 2.3 e quello delle azioni per 2.0. A confronto, l’indice basato sul PIL nominale assume nel 2015 un valore che è 2.2 volte quello del 1995 e per quello dei salari orari questo rapporto è 1.9. Si vede quindi che la crescita del valore delle attività finanziarie è stata molto più veloce di quella del valore dei flussi legati alla produzione corrente.
Grafico 12: Confronto fra diversi indici finanziari 1995-2015

In particolare, le attività finanziarie sono cresciute più velocemente del PIL al punto che il loro valore si è più che duplicato rispetto al PIL (2,2). Per gli attivi fissi, indicativi dell’evoluzione del valore dell’investimento “reale”, questo rapporto è invece di 1,2. Nello stesso periodo i salari nominali sono invece cresciuti meno rapidamente del PIL per cui hanno perso ancor più di quest’ultimo rispetto alle attività finanziarie.
Questi grafici documentano come nel corso degli ultimi decenni vi sia stato in parallelo un aumento del peso delle attività finanziarie rispetto al PIL e un’evoluzione sfavorevole della distribuzione dei redditi a scapito del lavoro. Non è questa la sede per entrare nel dettaglio di queste evoluzioni né per proporre un modello formale che le spieghi su basi circuitiste, ma la sostanza è abbastanza intuitiva: se si ammette che le banche o il sistema finanziario nel suo complesso possono creare liquidità (e/o quasi-liquidità) senza veri e propri limiti, è logico che questa si orienti verso le attività a rendimento più elevato. Se inoltre il sistema permette un afflusso costante di nuova liquidità verso i mercati finanziari (Toporowski, 2000, pp. 31-41), si possono creare le condizioni per guadagni in conto capitale che si auto-alimentano e che eccedono qualsiasi rendimento offerto dall’accumulazione tradizionale.
2.3 Uno sguardo agli aggregati macro-finanziari più recenti
Per completare il quadro empirico, in questa sezione si esaminano i dati relativi agli anni più recenti. Come argomentato in precedenza, la difficoltà per la valutazione empirica del circuito è che non si osserva la finanza iniziale[37]. Si osservano invece vari aspetti della finanza finale, in particolare i debiti e le liquidità accumulati a fine periodo, nonché il risparmio. Dal punto di vista conoscitivo, il punto interessante è ovviamente quello della causalità dei prestiti sui depositi. Come già detto, in quest’ottica si deve considerare che l’acquisto di un titolo da parte delle banche ha lo stesso effetto che un prestito, cioè crea moneta, senza però creare necessariamente un reddito, e questo può contribuire a spiegare le manifestazioni del processo di finanziarizzazione[38].
Le banche, e più in generale il sistema finanziario, acquistando e vendendo titoli all’interno del circuito del risparmio, possono quindi aumentare il loro prezzo determinando un aumento del valore dei beni accumulati nel passato rispetto ai valori della produzione corrente.
Alcuni grafici estesi al periodo più recente permettono una rapida verifica indiretta di questa e di altre delle principali idee del circuito. Nel primo grafico si osservano il PIL e il valore dei prestiti all’attivo degli intermediari finanziari e monetari della zona euro. Si nota una certa corrispondenza. Nel secondo grafico si riportano invece le stesse variabili in variazione e anche qui c’è una certa corrispondenza, anche se non è perfetta.
Grafico 13: Area Euro – Prestiti e GDP nominale: livello (sinistra) e variazione(destra) 1990Q1-2021Q1

Il terzo grafico riguarda le passività emesse dalle imprese sia sotto forma di prestiti che di titoli e li confronta al monte salari aggregato negli ultimi 15 anni. Sono evidenziati due sottoperiodi nei quali la riduzione dei prestiti accesi dalle imprese ha determinato una decelerazione dei salari.
Grafico 14: Area Euro – Indebitamento imprese (sin.) e prestiti delle banche (destra) 1990Q1-2021Q1

Nel quarto grafico che riprende in stock e in variazione le due componenti dei prestiti e dell’acquisto di titoli all’attivo delle banche della zona Euro, si vede che l’evoluzione dei titoli detenuti e dei prestiti è stata abbastanza correlata, che sia in livelli o in variazioni.
Grafico 15: Area Euro – Indebitamento delle imprese: rapporto tra flussi e consistenze: 1990Q1-2021Q1

Un fatto notevole è che il rapporto fra flussi e stock nel corso del tempo è andato riducendosi, come si vede nel grafico 15 qui accanto, che descrive l’evoluzione del debito al passivo delle imprese: i prestiti (F4) in blu e i titoli (F3) in arancione, entrambi espressi in percentuale dei valori dei rispettivi stocks. Si può innanzitutto osservare che questa percentuale è bassa: il valore della moneta presa a prestito durante l’anno è stato dell’ordine del due percento rispetto al valore dei debiti e dei prestiti accumulati, ed è sceso all’un percento negli anni successivi al 2009. Si osserva dunque nel corso del tempo una riduzione del valore dei flussi rispetto agli stocks, che è compatibile con una spiegazione dell’aumento del prezzo relativo degli attivi finanziari che rappresentano la ricchezza già accumulata rispetto ai flussi come il salario.
Grafico 16: Area Euro – Depositi delle e delle imprese in % del PIL: 1990Q1-2021Q1

Questo ultimo aspetto è confermato nel grafico 16 a sinistra che mostra come il rapporto tra depositi e PIL per le famiglie e le imprese dell’area Euro è aumentato quasi costantemente negli ultimi 25 anni, di circa uno per cento del PIL per le famiglie e di 0,5 punti percentuali del PIL per le imprese. A conferma indiretta della pertinenza del circuito, l’ipotesi di nullità delle variazioni delle scorte liquide non è quindi verificata empiricamente (cf. §1.1.2.2 e §1.1.2.5).
In conclusione, i test econometrici condotti nel 2008 per i paesi Visegrad hanno validato empiricamente la teoria del circuito monetario per questi paesi, cosa a priori non del tutto ovvia, trattandosi di economie allora e forse tuttora in transizione. Peraltro, posto che ciò che differenzia il circuito dagli approcci mainstream è l’aggiunta di un terzo polo bancario che crea moneta in maniera autonoma in funzione della redditività dei flussi di liquidità scontati dei vari investimenti possibili[39], l’esame di vari indicatori conferma che la teoria del circuito monetario è utile per capire le principali evoluzioni macro-finanziarie recenti e in particolare la caduta del prezzo relativo del lavoro rispetto a quello del risparmio a lungo termine che è poi una delle manifestazioni più significative della cosiddetta finanziarizzazione. Questa è legata all’aumento del valore degli stock finanziari raggiunto attraverso finanziamenti a leva che li privilegiano rispetto ai flussi legati alla produzione come i salari, meno appetibili per la finanza iniziale.
3. Il legame con la teoria del valore
Oltre al suo interesse teorico discusso nella prima parte e la sua capacità pratica a descrivere e spiegare un certo numero di fatti empirici, discussa nella seconda parte, l’interesse del circuito è anche quello di fornire un legame con la teoria del valore, che, come nella Teoria generale di Keynes, è un valore espresso in unità di salario (Graziani, 1983b), punto più volte sottolineato da Bellofiore (1989, 2018). Si accenna brevemente in quest’ultima parte al fatto che questo legame può servire per costruire un’analisi costi benefici “eterodossa”, infatti la non-neutralità della moneta circuitista implica anche una distinzione logica fra prezzi di conto, da usare per valutare l’impatto sociale degli investimenti finanziati, e prezzi di mercato, espressi in contanti.
Dando per scontato che il risultato neoclassico del rendement social di Allais (1943, 1981) è corretto, la variazione di benessere associata a un cambiamento dell’economia è data sostanzialmente dal prodotto delle quantità “incrementali” ΔQ per un prezzo “di conto” PC:
ΔWelfare=PC*ΔQ
Per Allais, questo prezzo deve essere quello di mercato, che si suppone uguale al prezzo neoclassico di equilibrio[40], ma in altri approcci può essere prezzo diverso. Ad esempio, la moneta endogena, che nel circuito è non-neutrale, porta a rifiutare l’idea che i prezzi relativi di equilibrio neoclassici possano essere dei prezzi di mercato. DQ è invece un “fatto” empirico da accertare caso per caso. Il problema per la valutazione sta nel come si calcola PC.
Il circuito si fonda sull’eguaglianza temporale e istantanea tra il valore V(Xt) della produzione Xt realizzata in un lasso di tempo e il valore dei redditi monetari creati per remunerare il lavoro impiegato a questo fine all’inizio di questo periodo. C’è quindi una corrispondenza temporale tra la moneta flusso creata al tempo t per fini produttivi ΔMt e il valore “sociale” V dei beni prodotti durante quel periodo:
ΔMt = V(Xt)=PC*ΔQ
relazione che somiglia a quella della teoria quantitativa della moneta ma che ha un’interpretazione totalmente diversa. Anche se non ci sono molti studi teorici né empirici che affrontano la questione da questo punto di vista, si possono prendere come punto di partenza i lavori di Vallageas (2010, 2018) che si propongono di correggere i prezzi “di produzione di mercato”, per il fatto per esempio che i profitti, nell’interpretazione di Schmitt a cui Vallageas si rifà sotto quest’aspetto, sono un puro trasferimento. La contabilità in “valore-salario” che egli sviluppa ha per effetto di correggere i prezzi di mercato e trasformarli in prezzi espressi in “valore-lavoro” e quindi apre una via che sotto certi aspetti si ricongiunge con l’auspicio espresso da Lesourne (1977) di sviluppare un’analisi costi-benefici espressa unicamente in termini di valore del tempo e che offre inoltre collegamenti suggestivi con la teoria classica del valore-lavoro [41]. Infatti, una volta chiarito meglio il legame fra valore della moneta creata per la produzione corrente e quello della moneta che finanzia l’acquisto di attività reali e finanziarie esistenti durante lo stesso periodo (cf. discussione nella seconda parte), lavoro che resta in gran parte da sviluppare, si può pensare a integrare gli schemi del circuito con quelli che discendono dall’interpretazione della teoria del valore-lavoro accolta da Pasinetti (Pasinetti & Garbellini, 2015). Questa linea di indagine si preannuncia laboriosa ma è molto interessante e potenzialmente feconda di risultati utili. Si può avvalere anche della riflessione avviata da tempo su questi temi da Riccardo Bellofiore (1989, 2018).
Conclusione
Nel modello del circuito monetario:
- Le banche e la moneta hanno esistenza e funzioni proprie. Il modello è particolarmente adatto a interpretare realisticamente fenomeni monetari legati a nuovi prestiti o impieghi.
- C’è un fondamento macroeconomico della microeconomia. “I prestiti creano i depositi” e altre proposizioni collegate, che implicano catene di causalità alternative per valutare gli effetti della politica economica monetaria e finanziaria, sono verificate e/o verificabili empiricamente. Il modello può servire anche a spiegare la formazione di rendite finanziarie.
- Al centro dell’analisi c’è il legame tra prestiti, moneta e distribuzione del reddito che è cruciale per capire gli effetti sociali della politica economica. Si sa che, fuori dall’equilibrio neoclassico, allocazione e distribuzione non sono indipendenti, ciò che richiede un’impostazione economica del problema della distribuzione che sia aperto rispetto ad analisi multidisciplinari che ne spieghino gli aspetti extra-economici. A questo scopo, il circuito suggerisce l’uso di quadro di riferimento basato sulla teoria del valore-lavoro per valutare l’effetto sociale delle operazioni bancarie.
- Nella versione che ha sviluppato Graziani in maniera autonoma e originale[42], il circuito è compatibile con quello degli altri autori capostipiti dell’approccio che sono Schmitt, Parguez e Poulon che completano le sue analisi con risultati complementari (Cingolani, 2023).
In conclusione, per tutte queste ragioni, il circuito monetario è un approccio che appare ineludibile per valutare gli effetti economici e sociali dell’attività bancaria ed è quindi uno schema di indubbia utilità che va approfondito e sviluppato.
Sia consentito in chiusura un commento su come inquadrare il circuito nel resto della produzione scientifica e culturale di Augusto Graziani. Graziani è stato un economista completo col pallino della macroeconomia e un grande esperto di moneta e politica monetaria. Ha affrontato tutti i problemi più difficili della teoria economica armato della sua grande cultura e profonda conoscenza della storia del pensiero economico, nutrita dalla sua lettura attenta dei classici economici in lingua originale. Fin dall’inizio della sua carriera di docente, si è interessato ai problemi di analisi costi benefici (Graziani, 1961) con largo anticipo sui primi manuali che l’OCSE e la Banca Mondiale dedicheranno al tema alla fine degli anni Sessanta, restringendolo progressivamente al solo ambito neoclassico. Il suo rigore intellettuale lo ha portato a rigettare l’analisi neoclassica del capitale già nel 1965, contribuendo indirettamente e in maniera discreta a nutrire un dibattito importante e generalmente trascurato che ha coinvolto all’epoca i principali economisti neokeynesiani e post-keynesiani delle due sponde dell’atlantico (Graziani, 1965, discusso in Cingolani, 2016).
Ma la sua mente fertile non si interessava solo di questioni teoriche. Oltre a formare diverse generazioni di studenti, molto dei quali sono diventati a loro volta docenti o dirigenti in Italia e all’estero, dedicava grande attenzione alla storia (Graziani, 1975) ed è stato un cittadino fortemente impegnato nel dibattito politico e civile. In particolare, ha dedicato molte delle sue energie ad affrontare concretamente i difficili problemi dello svilluppo del Mezzogiorno italiano (Graziani, 2020) animando tra l’altro insieme a Rossi la celebre scuola di Portici (Costabile, 2004) che ha contribuito a formare una parte rilevante della classe dirigente economica nazionale.
È probabilmente dal confronto tra l’osservazione attenta della realtà nelle sue sfaccettature più problematiche e la sua profonda conoscenza della dottrina economica che è nata l’intuizione del circuito monetario che è uno dei suoi contributi più originali e fecondi. Come si è cercato di mostrare, questo schema offre una chiave semplice e rigorosa per ragionare sui fatti monetari e finanziari, che ha rilevanza empirica ed è fertile di possibilità di sviluppo future.
[1] Banca europea per gli investimenti. Le idee espresse lo sono a titolo personale. Testo scritto per il blog del sito dedicato ad Augusto Graziani (Blog Graziani) che rielabora una presentazione online per la Rete Italiana Post-Keynesiana nel quadro di una “Lezione sul pensiero di Augusto Graziani” organizzata con Riccardo Bellofiore l’ 8.4.2022 (IPKN Lezione Graziani). Il testo derivato da questa presentazione è stato poi discusso in un convegno a Bordeaux il 6-7 dicembre 2022 (“Circuit et modélisation macro-économique de la transition écologique: I. Fondements et actualité du circuit”). Versioni precedenti di questo testo hanno beneficiato di commenti e/o incoraggiamenti da parte di Riccardo Bellofiore, Eric Berr, Marcella Corsi, Jean-Paul Guichard, Marc Lavoie, Edwin Le Héron, Matthieu Llorca, Fréderic Poulon, Louis-Philippe Rochon, Sergio Rossi, Mario Seccareccia e Bernard Vallageas che sono calorosamente ringraziati. L’autore resta responsabile di tutti gli errori rimanenti. Versione datata 28 aprile 2023.
[2] In questa definizione, de Finetti non si sofferma sulla distinzione che si fa talvolta, specie nella letteratura antropologica, fra moneta e denaro. Si ringrazia Riccardo Bellofiore per avere segnalato all’autore che anche Graziani (1983a, p. 225) fa questa distinzione, che introduce per illustrare il concetto marxiano di moneta come equivalente generale, per cui Graziani contrappone la ricchezza in generale (denaro) alla ricchezza liquida (moneta). La distinzione tra i due concetti è importante e molto attinente al tema qui trattato, ma si può osservare che i principali dizionari italiani tendono a trattare moneta e denaro come sinonimi riprendendo l’uso della lingua parlata nella quale per denaro non si intende la ricchezza in generale. Comunque, accogliendo questa distinzione, le operazioni finanziarie hanno per oggetto scambi “in moneta contante”.
[3] Non è del tutto ovvio definire cos’è il mainstream (o pensiero egemonico) in economia, eccetto che come l’insieme di dottrine che più incidono sulle decisioni collettive. Un punto che in genere caratterizza tutti questi approcci, che a bene vedere sono molto diversi fra loro, è che tendono a interpretare normativamente i prezzi di mercato, e quindi considerarli come prezzi “naturali”, per cui la distribuzione dei redditi e delle ricchezze diventa un dato esogeno che esula di fatto dall’analisi economica. Riccardo Bellofiore ha osservato che le politiche odierne sono soprattutto ispirate alla scuola austriaca che è per lui eterodossa. Certamente molti degli autori “neo-austriaci” si considerano e vengono considerati eterodossi; tuttavia, Hayek resta pur sempre uno dei tre capostipiti dell’equilibrio economico generale moderno e quindi a giudizio di chi scrive la sua scuola si può annoverare nel mainstream. Peraltro, nella vulgata economica dominante si mescolano in un unico calderone elementi neoclassici, monetaristi e neo-austriaci, generando una confusione che rende il dibattito economico totalmente incomprensibile al pubblico non specialistico, ma uno dei pochi punti di accordo è appunto lo slogan: “You have got to get your prices right”.
[4] Nel testo si parla soprattutto di famiglie piuttosto che di lavoratori e di imprese piuttosto che di capitalisti seguendo la terminologia in uso in contabilità nazionale. Per quanto, come rileva Riccardo Bellofiore, questa terminologia non sia a rigore applicabile al modello di Graziani, dove i settori coincidono con le classi sociali degli economisti classici, il riferimento alla contabilità nazionale è giustificato perché da un lato lo sviluppo del circuito monetario è sempre stato molto legato ed ha influenzato quello della contabilità nazionale e dei flussi di fondi, specie nella tradizione francese (Denizet, 1972; Poulon, 2015, pp. 95-150, Berr & Monvoisin, 2023), e dall’altro qualsiasi verifica empirica del circuito poggia sui concetti e aggregati di contabilità nazionale.
[5] Nei modelli neoclassici che integrano le banche, queste svolgono un ruolo passivo di intermediazione fra il risparmio e l’investimento (Graziani, 2003, pp. 74-81). La moneta è uno stock la cui creazione è devoluta al solo settore pubblico che la effettua attraverso i suoi disavanzi di bilancio (Graziani, 1984a, p. 127). Da qui deriva l’idea che ha dominato le politiche economiche occidentali dopo gli anni Settanta di ridurre il deficit pubblico per evitare l’inflazione di origine monetaria. Come proposto da Milton Friedman, lo scopo era quello di stabilizzare la quantità di moneta in circolazione controllando il tasso di crescita della base monetaria, che avrebbe dovuto rimanere costante. Queste politiche sono state abbandonate abbastanza rapidamente perché si sono rivelate impossibili da mettere in atto, ma le idee che le sottendono restano dominanti, come testimoniano i dibattiti odierni sul ritorno dell’inflazione.
[6] In macroeconomia un modello si compone generalmente di un certo numero di equazioni che legano fra loro variabili diverse, alcune spiegate dal modello stesso, altre considerate come date. Un blocco all’interno di un modello corrisponde a un sottogruppo di equazioni che tratta fenomeni collegati, ad esempio il blocco del consumo, quello della produzione o quello dei prezzi e dei salari. In genere le equazioni di un blocco sono logicamente distinte dalle altre e la loro soluzione può essere esaminata separatamente da quella del resto del modello (Deleau e Malgrange, 1978). Nella generazione dei modelli macro-econometrici Keynesiani degli anni Settanta, che ha svolto un ruolo importante nella gestione economica delle “trente glorieuses”, il blocco monetario e finanziario era notoriamente il più carente. Constatata la difficoltà di questi modelli a spiegare la moneta e la macro-finanza, a partire dagli anni Ottanta si è pensato di escludere totalmente la moneta e le banche dai modelli macro-econometrici, come nei modelli cosiddetti DGSE (Dynamic Stochastic General Equilibrium Models) tuttora in uso presso diverse banche centrali e istituzioni internazionali. Un’alternativa più feconda sarebbe stata invece quella di seguire la via indicata da Graziani e introdurre la moneta all’interno di questi modelli a partire da una comprensione dettagliata del suo funzionamento, piuttosto che ignorarla. Va precisato a riguardo che, malgrado i loro limiti teorici, le proiezioni dei modelli DGSE possono comunque essere attendibili, e per questo vengono usati, dato che è sempre possibile calibrarli con una precisione data sui dati reali. Il problema è però che quando vengono usati per delle simulazioni in variante, trascurano quella parte ignota del meccanismo di trasmissione della politica monetaria che è incluso nel fattore di aggiustamento usato per calibrare il modello, che è poi il “residuo” (diverso da zero) usato in proiezione per ottenere la simulazione di controllo (“la previsione”), talvolta indicato anche come “add-factor”.
[7] Ovviamente né Graziani, né i principali circuitisti e post-keynesiani o i neoclassici lo hanno mai fatto.
[8] Al contrario e tipicamente nei modelli neoclassici, la macroeconomia è data dalla somma dei comportamenti microeconomici individuali (Malinvaud, 1956), il che preclude in ultima analisi ogni possibilità di disoccupazione involontaria. Per un collegamento con la controversia sul capitale, si veda Seccareccia (1982).
[9] Generalmente illustrata dicendo che non sono le stesse persone che risparmiano e che investono, che sono gli investimenti che creano i risparmi, o che il risparmio liquido del singolo, a lui benefico, è un danno per la collettività.
[10] La versione “insiemistica” o anche “topologica” si riferisce all’equilibrio generale di Arrow-Debreu ed è più astratta e usa una matematica meno comprensibile di quella tradizionale neoclassica di Walras e Pareto, basata su modelli a equazioni simultanee, ma conferma e specifica più rigorosamente il dominio di validità dei suoi risultati.
[11] Anche se i modelli simultanei sono usati regolarmente per discutere di politica economica, dato che tutto avviene allo stesso tempo, in realtà non si sa quale variabile causa quale altra, eccetto nel caso abbastanza raro in cui sono totalmente ricorsivi e quindi sequenziali sul piano logico (Pasinetti, 1965).
[12] L’autore è in debito con Riccardo Bellofiore per avergli segnalato questa introduzione, come quella altrettanto fondamentale al libro di Convenevole (Graziani, 1977).
[13] “Equilibrio” va qui inteso nell’accezione di “soluzione del modello” (Deleau & Malgrange, 1978) e quindi non significa necessariamente “prezzo=costo marginale”. Nel circuito quest’equilibrio può coincidere solo con la variazione nulla delle scorte liquide. L’autore è grato a Louis-Philippe Rochon per aver insistito sulla necessità di questo chiarimento.
[14] Sia consentita una piccola digressione. Le formulazioni originali della teoria di Kalecki in polacco e in tedesco precedono la Teoria Generale, ciò che ha fatto dire ad alcuni esperti che Keynes avrebbe “copiato” Kalecki su questo punto. Altri esperti obiettano che dato che Keynes non parlava né polacco, né tedesco, le scoperte di questi due maestri sono state indipendenti. L’autore è grato a Jean-Paul Guichard per avergli segnalato che se Keynes non avesse capito il tedesco, non avrebbe potuto scrivere il Trattato sulla Probabilità (che in effetti discute in dettaglio tutta la letteratura probabilistica e attuariale tedesca dell’Ottocento), e che le idee principali di Kalecki erano state presentate nel 1935 in francese a un congresso della società di econometria al quale Keynes aveva partecipato. Non si può quindi escludere che Keynes fosse venuto a conoscenza delle idee principali di Kalecki, anche se parlare di plagio è forse eccessivo.
[15] Graziani (1983 e 1984a) argomenta che questa separazione differenzia i due principali filoni della letteratura monetaria che si possono ricondurre a Fisher e Friedman da un lato, che sostengono che l’interesse monetario si adatta pienamente all’inflazione, e dall’altro a Wicksell, Keynes e Robertson, che contestano la veridicità dell’indicizzazione totale dei tassi di interesse all’inflazione.
[16] Per usare la tassonomia proposta da Musgrave (1981), citato da Salanti (1985), ignorare le variazioni delle scorte di moneta, è, come mostra il modello del circuito, un’ipotesi “non-trascurabile” (“non-negligible”), nel senso che il suo abbandono modifica la causalità fra le principali variabili macroeconomiche (Cingolani, 2022a, p. 256 e seguenti).
[17] Come osservato, per il circuito, la moneta è una passività emessa da un terzo estraneo alla transazione (acquisto o vendita) che viene accettata dalle due parti proprio perché il terzo (Stato, banche, o persona facoltosa) è un’entità “credibile” a loro estranea. Questa definizione esclude che i cosiddetti “I Owe You” siano moneta, non si può cioè pagare con proprie promesse di pagamento o, se si fa, queste non sono moneta. Per la stessa ragione, i bitcoins non sono moneta in senso circuitista perché sono un’attività e non una passività, sono cioè beni che hanno un valore più o meno permanente, sia esso speculativo (materie prime), collezionistico (francobollo) o artistico, ma che non deve normativamente scomparire al momento della chiusura del circuito, come la “vera moneta” circuitista.
[18] Parguez parte da un modello minimo in cui figura anche lo Stato, perché per lui senza di esso non si può concepire lo “spazio della moneta”. Graziani invece, seguendo in questo Wicksell, fa la scelta più radicale di iniziare il ragionamento da un modello in cui c’è solo il settore privato, ciò che gli permette di illustrare come la classe sociale dei capitalisti, avendo accesso al credito, decide l’allocazione delle risorse fra consumo e investimenti. Parguez, e in generale i circuitisti francesi, ammettono l’esistenza di una moneta di “secondo rango” emessa dalle banche private a favore dei capitalisti, ma questa è logicamente (perché legalmente) inferiore alla moneta di primo rango emessa dalla Banca Centrale, che è la sola “vera moneta”. La gerarchia fra moneta di primo e secondo rango (base monetaria e M1), non viene contestata da Graziani, ma il fatto di adottare un’ipotesi teorica più drastica, gli permette di illustrare le condizioni minime per l’esistenza della moneta, fra cui non c’è per lui l’esistenza della Stato. Si trovava comunque probabilmente d’accordo con Parguez quando questi ironizzava sul fatto che il debito pubblico è “oro” per l’attivo di bilancio di una banca, come aveva a suo tempo osservato il banchiere, parlamentare francese e fondatore del Crédit Lyonnais Henri Germain (Cingolani, 2013).
[19] Questo raggruppamento delle equazioni non c’è come tale in Graziani, anche se è una conseguenza relativamente ovvia della sua analisi. Esplicitarla illustra il funzionamento del blocco monetario e finanziario del circuito che, integrando la moneta endogena, ribalta le relazioni causali dei principali modelli macroeconomici quando viene ad essi integrato.
[20] Come giustamente fatto rilevare da Marc Lavoie, se il livello dell’occupazione come quello della produttività sono dati, in effetti è dato anche il livello della produzione X che non è quindi strettamente endogeno. Oltre che per disporre di una relazione che rispetti la linearità dei coefficienti di produzione assunta da Graziani come da molta della letteratura post-keynesiana, si è scelto di trattare l’output come endogeno e l’impiego come esogeno per evidenziare che nel circuito di Graziani le imprese decidono sia il livello dell’occupazione e quindi della produzione, che la sua ripartizione fra beni di consumo e beni di investimento. Si potrebbe dire che le imprese hanno quasi l’imbarazzo della scelta fra le variabili che sono sotto il loro controllo per definire ogni aspetto del ciclo di produzione e distribuzione. Tale libertà deriva dal fatto che le banche mettono a loro disposizione il potere d’acquisto necessario per realizzare i propri piani. Le famiglie lavoratrici non hanno invece un simile accesso al credito per la creazione di reddito. Possono solo decidere il livello del loro risparmio come frazione del reddito che le imprese hanno deciso di distribuire loro. Le imprese sono a loro volta di fatto subordinate al settore bancario al quale devono destinare una parte dei profitti sotto forma di interessi. Al conflitto capitale lavoro per la ripartizione tra salari e profitti, si sovrappone quindi, e in effetti prevale in Graziani, quello fra imprese e banche per la ripartizione fra profitto e interesse.
[21] Graziani (2003, p. 102) osserva anche che il livello dei prezzi non dipende dalla quantità di moneta, che è totalmente endogena nel circuito.
[22] Lettura che Alain Parguez considerava insuperata (comunicazione personale).
[23] Il che dimostra en passant l’interesse della scomposizione in fasi del periodo di produzione del circuito fatta da Graziani.
[24] In effetti compatibile a sua volta con gli schemi di riproduzione di Marx, ciò che non dovrebbe sorprendere più di tanto alla luce dell’analisi di Barone (1908).
[25] È noto che Kalecki non abbia mai scritto questa frase che gli è stata attribuita da Kaldor e Robinson.
[26] Le relazioni (10) e (12) sono leggermente modificate rispetto a quelle presentate da Graziani, per ottenere delle unità di misura più intuitive: 1+β è usato al posto di β e 1+μ è usato al posto di μ.
[27] In effetti la (10) si può ricavare da bd=iB ⁄ [(1+β)2 iD2 ] per la domanda di risparmio in titoli delle famiglie e da bs=(i_L2)⁄[(1+μ)2 iB2 ] per l’offerta di titoli delle imprese quando bd=bs.
[28] In questo caso, la condizione di equilibrio sul mercato finanziario che postula l’eguaglianza fra domanda e offerta di titoli delle imprese in proporzione al risparmio (che Graziani scrive genericamente: bd[iB/iD]=bs[iL/iB]=b) è posta uguale a uno (Graziani, 2003 pp. 124 e p. 127), il che implica anche una variazione nulla delle scorte liquide. Il caso è dunque quello di “moneta senza crisi” (Graziani, 1984b) e non quello “Malthusiano” (Graziani, 1980), in cui la moneta spiega il principio della domanda effettiva.
[29] Fra le esogene bisognerebbe a rigore distinguere i parametri di comportamento o tecnologici (b, s, b, m, e p), dal resto delle esogene (N, iD, iL, w), ma qui i due gruppi sono trattati insieme dato che di fatto tutti questi sono dei valori assunti come costanti nel periodo del circuito e che determinano le variabili endogene.
[30] La soluzione rispetta le identità seguenti: p*X = C+I = Y + P; Y = C + S = W + iB*B + ; S = B + DL; I = S + P.
[31] La figura corrisponde a quella presentata da Graziani (2003, p. 127). Un’inversione semantica, che è forse un refuso di stampa o una distrazione, è stata corretta nel commento che segue. Comunque, è ininfluente ai fini dell’argomentazione.
[32] L’esplicitazione del conflitto distributivo fra banche e imprese è uno dei contributi più interessanti e fecondi dell’analisi di Graziani e gli ha consentito di dimostrare come l’identità di Fisher secondo la quale il tasso di interesse nominale sarebbe la somma del tasso di interesse reale e del tasso di inflazione non è necessariamente valida a seconda che la creazione monetaria venga dal deficit pubblico oppure dalla creazione di moneta bancaria (Graziani, 1983a e 1984a), analisi che conferma quanto sopra e sulla sottilità della quale l’attenzione dell’autore è stata attirata a suo tempo da Alain Parguez.
[33] Il materiale presentato in questa sezione è stato preparato per una tavola rotonda del SIOI nel 2017 e per questo motivo i dati esaminati arrivano al 2016. “Riflessioni su moneta e finanza nello spazio europeo”, Tavola rotonda su L’Europa a geometria variabile: aspetti economici, monetari e di sicurezza, 3 ottobre 2017, Roma: SIOI. È poi stato usato anche in conferenze svoltesi lo stesso anno a Venezia e a Grenoble. “Financial assets dynamics in industrialized countries: trends and implications: A critical review of the financial balance sheets of the main industrial countries”, Interest Rates, Growth and Regulation, Venezia: 28-29 settembre 2017; e: “Financial assets dynamics in industrialized countries: trends and implications”, International Post-Keynesian and Institutionalist Conference on “Instability Growth & Regulation”, Grenoble: December 7-9, 2017.
[34] Perché ciò avvenga basta che il “tempo” del circuito finanziario sia più breve di quello del circuito “reale”, come elaborato nella conclusione al §2.2. Si ammette quindi implicitamente che in un dato periodo si possano svolgere due circuiti: uno è quello “canonico” relativo alla generazione del reddito (ricchezza reale) e uno è quello finanziario “degli scambi di denaro “. Quest’idea è sviluppata schematicamente in Cingolani (2013, p. 283) e in Cingolani (2019, p. 283) dove viene usata per discutere e interpretare rispettivamente l’evoluzione delle variabili macro-finanziarie europee e il ruolo della banca pubblica. In Cingolani (2022b, pp. 20-27) si sviluppa invece un esempio di articolazione delle fasi del periodo singolo del circuito per discutere il problema del finanziamento privato delle attività ambientali.
[35] Si è scelto questo valore iniziale arbitrario come parametro per distinguere meglio le curve sul grafico in funzione delle rispettive scale.
[36] A rigore il paragone porta su delle velocità delle dinamiche del valore di mercato, ma accettando un’ipotesi semplificatrice di omogeneità dei panieri di “quantità” di tali attivi, si può attribuire la maggior parte della variazione dei valori relativi ai prezzi di queste attività, anche perché nel campo dei prodotti finanziari non ha molto senso distinguere la quantità dal prezzo.
[37] Guardando ai flussi di finanziamento lordi, si ha un’indicazione della finanza “inizialmente consentita” ma in genere non si osservano i prestiti richiesti inizialmente dalle imprese ma rifiutati dalle banche, quelli cioè che rappresentano la loro “vera” percezione della domanda effettiva.
[38] Come osservato nella sezione precedente, si veda anche Cingolani (2013).
[39] Cioè in maniera “endogena” rispetto al funzionamento del sistema economico e ai suoi bisogni di liquidità.
[40] Anche se in genere non entra esplicitamente in queste discussioni, sembra lecito affermare che Allais, uno dei massimi teorici dell’analisi del welfare, presume l’applicabilità al mondo reale dell’ottimo di primo rango (first best), che è di equilibrio in quanto risultante da una massimizzazione vincolata e, essendo “ottimale”, induce a ritenere che qualsiasi deviazione rispetto a quest’ottimo sia “di secondo ordine”. Nelle analisi empiriche sui costi-benefici, si tende invece a separare prezzi di conto (o prezzi ombra) e prezzi di mercato, cosa che è esclusa dalla finanza moderna che postula invece possibilità di arbitraggio infinite.
[41] Il fatto che la liquidità creata dai prestiti nel finanziamento iniziale rappresenti i redditi salariali prefigura una possibile integrazione con la teoria del valore-lavoro sviluppata da Pasinetti (1986 e 1993) sulla scia delle analisi di Sraffa.
[42] Come ben spiegato da Riccardo Bellofiore nella sua lezione Graziani per IPKN e in Bellofiore (2013 e 2019). In generale, sull’apporto di Graziani, oltre agli eccellenti contributi pubblicati su questo blog, si vedano tra gli altri gli ottimi Fausto (2014), Costabile (2015) e Giannola (2020).
Riferimenti
-
Allais, Maurice. [1943] 1994). A la recherche d’une discipline économique, pubblicato col titolo Traité d’Économie Pure, Paris: Clément Juglar.
-
Allais, Maurice. [1981] 1989. La théorie générale des surplus : nouvelle édition précédée d’un avant-propos de l’auteur. Grenoble : Presses Universitaires de Grenoble (première édition : Economies et Sociétés Cahiers de l’ISMEA n. 1 à 5, 1981)
-
Barone, Enrico. 1908. “Il ministro della produzione nello stato collettivista”, Giornale degli Economisti, Serie Seconda, Vol. 37 (Anno 19), Settembre: pp.267-293. e “[…] Continuazione”, ibid., Ottobre: 391-414.
-
Bellofiore Riccardo. 1989. “A Monetary Labour Theory of Value”, Review of Radical Political Economics, 21, n. 1-2: 1-25.
-
Bellofiore, Riccardo. 1998. “Between Wicksell and Hayek: Mises’ Theory of Money and Credit Revisited”, American Journal of Economics and Sociology, Vol. 57, No. 4 (Oct.), pp: 531-578.
-
Bellofiore, Riccardo. 2013. “A heterodox structural Keynesian: honouring Augusto Graziani”, Review of Keynesian Economics, Vol. 1 No. 4 (Winter), pp. 425–430.
-
Bellofiore, Riccardo. 2018. Le avventure della socializzazione. Dalla teoria monetaria del valore alla teoria macro-monetaria della produzione capitalistica. Milano: Mimesis.
-
Bellofiore, Riccardo. 2019. “Augusto Graziani and the Marx-Schumpeter-Keynes ‘Cycle of Money Capital’: A Personal Look at the Early Italian Circuitism from an Insider”, Review of Political Economy, 31:4, 528-558
-
Bellofiore, Riccardo. 2022. “La moneta come capitale. Augusto Graziani e il primo circuitismo: 1975-1985”, Intervento alla Lezione sul pensiero di Augusto Graziani, evento online organizzato dall’Italian Post Keynesian Network il 8.04.2022: IPKN Lezione Graziani.
-
Berr, Éric & Virginie Monvoisin. 2023. “Modern post-Keynesian approaches: continuities and ruptures with monetary circuit theory”, Journal of Post Keynesian Economics, 2023, DOI: 10.1080/01603477.2023.2167092
-
Cingolani, Massimo. 2013a. “The monetary conditions for growth: Parguez’s debt stability condition”, Ch. 14 in: Monetary Economies of Production. Banking and Financial Circuits and the Role of the State, Louis-Philippe Rochon and Mario Seccareccia ed., pp. 205-234, Cheltenham UK: Edward Elgar.
-
Cingolani, Massimo. 2013b. “Finance Capitalism: A Look at the European Financial Accounts”, Panoeconomicus, 2013, 3, Special Issue, pp. 249-290.
-
Cingolani, Massimo. 2016. “Augusto Graziani’s Equilibrio generale ed equilibrio macroeconomico: A key milestone in a long journey out of the neoclassical mainstream”, Review of Keynesian Economics, Vol. 4 No. 3, Autumn 2016, pp. 279–302.
-
Cingolani, Massimo. 2019. “Necessary Public Investment: The Role of Public Banks”, International Journal of Political Economy, 48:3, 275-300.
-
Cingolani, Massimo. 2022a. “What Economic Modelling Hypotheses Should Underlie Regulation & Policy Advice? Towards a Probabilistic Approach”, Forum for Social Economics, 2022, Vol. 51, N. 3, 253–284.
-
Cingolani, Massimo. 2022b. “Public and Private Financing of Sustainable Development Goals (SDGs)”, Review of Political Economy, forthcoming.
-
Cingolani, Massimo. 2023. “The monetary circuit in Graziani, Parguez, Poulon and Schmitt: normative and positive implications”, intervento alla 49th Eastern Economic Association Annual Conference, New York 23-26 February 2023.
-
Costabile, Lilia. 2004. Il Centro di Specializzazione e Ricerche Economico-Agrarie per il Mezzogiorno e la ‘Scuola di Portici'”, in: La formazione degli economisti in Italia (1950-1975), a cura di Giuseppe Garofalo e Augusto Graziani, Bologna: Il Mulino.
-
Costabile, Lilia. 2015. “Augusto Graziani: Theoretician, Applied Economist, Historian of Economic Thought: An Appraisal”, Italian Economic Journal, n. 1 :155–170
-
de Finetti, Bruno. [1935] 1991. “Sulle operazioni finanziarie”, Giornale dell’Istituto Italiano degli Attuari, Roma, 1935, Anno VI, n. 4, pp. 289-302 In: Scritti 1931-1936, Bologna: Pitagora editrice.
-
Deleau, Michel e Pierre Malgrange. 1978. L’analyse quantitative des modèles macroéconomiques quantitatifs, Paris : Economica.
-
Eichner, Alfred S. 1973. “A Theory of the Determination of the Mark-Up under Oligopoly.”, Economic Journal, 83 n. 332: 1184–1200.
-
Eichner, Alfred. S. 1991. The macrodynamics of advanced market economies. Armonk, N.Y.: Sharpe.
-
Fausto, Domenicantonio (2014), “Augusto Graziani: a profile”, Studi Economici dell’Università degli Studi di Napoli Federico II, VXIX (112), 10–28, Special issue on ‘The Scientific Work of Augusto Graziani’, riprodotto in Accademia Nazionale dei Lincei.
-
Giannola, Adriano. 2020. “Introduzione” ad Augusto Graziani: Mercato, Struttura, Conflitto: Scritti su economia italiana e Mezzogiorno: 11-41.
-
Graziani, Augusto. 1961. La teoria delle scelte negli investimenti pubblici. Napoli: Casa editrice Dott. Eugenio Jovene.
-
Graziani, Augusto. 1965. Equilibrio generale ed equilibrio macroeconomico, Napoli: Edizioni Scientifiche Italiane.
-
Graziani, Augusto. 1975. Crisi e ristrutturazione nell’economia italiana. Torino: Einaudi.
-
Graziani, Augusto. 1977. “Recensione a mo’ di premessa”, Introduzione a: Processo inflazionistico e redistribuzione del reddito, R. Convenevole, Torino: Einaudi, XI-LVI.
-
Graziani, Augusto. 1980. “Malthus e la teoria della domanda effettiva”, Introduzione a Malthus. Sviluppo e ristagno della produzione capitalistica, Lilia Costabile, pp.: VII-LV, Torino: Giulio Einaudi, Editore, 1980.
-
Graziani, Augusto. 1981. “Keynes e il Trattato sulla moneta”, In Studi di economia Keynesiana, 211-234, a cura di Augusto Graziani, Cesare Imbriani e Bruno Jossa, Napoli, Liguori editore.
-
Graziani, Augusto. 1983a. “Interesse monetario e interesse reale. Storia di una controversia”, Rivista Milanese di Economia, n. 6: 77-108.
-
Graziani, Augusto. [1983b] 1997a. “Moneta e credito nell’economia marxiana”, in: I conti senza l’oste: Quindici anni di economia italiana, Torino: Bollati Boringhieri, pubblicato originariamente su Rinascita, nn. 50-51, 23 dicembre 1983.
-
Graziani, Augusto. [1983c] 1997b. “Riabilitiamo la teoria del valore”, I conti senza l’oste, 235-240, Torino: Bollati Boringhieri. Originariamente in L’Unità, 27 febbraio 1983, supplemento speciale per la morte di Karl Marx.
-
Graziani, Augusto. 1984a. “Interesse monetario e interesse reale”, In: L’interesse reale e monetario, a cura di Giacomo Costa, Alfredo del Monte, Adriano Giannola, Augusto Graziani, Ferruccio Marzano, Milano: Franco Angeli.
-
Graziani, Augusto. 1984b. “Moneta senza crisi”, in Studi Economici, XXXIX, n. 3, 1984, pp. 3-37.
-
Graziani, Augusto. 1984c. “The Debate on Keynes’s Finance Motive.”, Economic Notes, n. 1: 15-33.
-
Graziani, Augusto. 1987. “Keynes’ Finance Motive”, Economies et Sociétés – Série Monnaie et Production, XXI, n. 9 : 23-42.
-
Graziani, Augusto. 1994. “Real Wages and the Loans-Deposits Controversy”, Economie Appliquée, tome XLVl, n° 1, p. 31-46.
-
Graziani, Augusto. 1996. “Money as Purchasing Power and Money as a Stock of Wealth in Keynesian Economic Thought”, In: Money in Motion: The Post Keynesian and Circulation Approaches, Ghislain Deleplace & Edward J. Nell ed. London: Macmillan Press Ltd & New York: St. Martin’s Press Inc.
-
Graziani, Augusto. 2001. Teoria Economica, Macroeconomia. Quinta edizione riveduta e ampliata, Napoli: Edizioni Scientifiche Italiane.
-
Graziani, Augusto. 2002. “New lines of research in monetary economics”, Ch.11 in Is There Progress in Economics? Knowledge, Truth and the History of Economic Thought, Stephan Boehm, Christian Gehrke, Heinz D. Kurz & Richard Sturn ed., pp.173-192, Cheltenham, UK: Edward Elgar.
-
Graziani, Augusto. 2003. The Monetary Theory of Production, Cambridge: Cambridge University Press.
-
Graziani, Augusto. 2020. Mercato, Struttura, Conflitto: Scritti su economia italiana e Mezzogiorno. A cura di Adriano Giannola, Bologna: Il Mulino.
-
Hendry, David. F. & Jean-François Richard. [1982] 1993. “On the formulation of empirical models in dynamic econometrics”, Journal of Econometrics, 20 (1982) 3-33, reprinted in Econometrics: Alchemy of Science, Oxford: Blackwell Publishers.
-
Kalecki, Michal. 1942. “A Theory of Profits”, The Economic Journal, Vol. 52, No. 206/207 (Jun. – Sep.), pp. 258-267.
-
Lesourne, Jacques. 1977. A theory of the individual for economic analysis, Amsterdam & New York: North-Holland.
-
Llorca, Matthieu Jean-Paul Guichard and Cingolani, Massimo. 2009. Évolutions des agrégats macro-financiers dans les Nouveaux Pays Membres et Candidats à l’UE, STAREBEI research report, 181 p.
-
Malinvaud, Edmond. 1956. “L’agrégation dans les modèles économiques”, Cahiers du Séminaire d’Économétrie, No. 4 (1956), pp. 69-146.
-
Michell, Jo & Jan Toporowski. 2013-14. “Critical Observations on Financialization and the Financial Process”, International Journal of Political Economy, special issue on Understanding Financialization: History, Theory and Institutional Analysis, Vol. 42, No. 4 (Winter): pp. 67-82.
-
Mockers, Jean-Pierre. 2016. Court traité d’économie et de politique économique : Bonne théorie : Bonne politique ; mauvaise théorie : … ,Paris: L’Harmattan.
-
Parguez, Alain. 1996. “Beyond Scarcity: A Reappraisal of the Theory of the Monetary Circuit”, In: Money in motion: The Post-Keynesian and Circulation Approaches, Ghislain Deleplace & Edward Nell ed., London: Macmillan.
-
Parguez, Alain & Mario Seccareccia. 2000. “The credit theory of money: the monetary circuit approach”, In: What is Money, John Smithin ed., pp. 101-123, New York and London: Routledge.
-
Pasinetti, Luigi L. 1965. “Causalità e interdipendenza nell’analisi econometrica e nella teoria economica”, in: Annuario dell’Università Cattolica del S. Cuore, 1964-’65, 233-250, Bologna: Il Mulino.
-
Pasinetti, Luigi. L. 1986. “Theory of value. A source of alternative paradigms in economic analysis”. In: Foundations of Economics: Structures of Inquiry and Economic Theory, Mauro Baranzini & Roberto Scazzieri eds., pp. 409–431. Basil Blackwell.
-
Pasinetti, Luigi L. 1993. Structural economic dynamics: a theory of the economic consequences of human learning, Cambridge: Cambridge University Press.
-
Pasinetti, Luigi L. & Nadia Garbellini. 2015. “From Sraffa: Backwards, To a Better Understanding of Marx’s Values/Prices “Transformation”; and Forward, To a Novel View of Growing Economic Systems”, Cahiers d’économie politique / Papers in Political Economy, n. 69, What have we learnt on Classical economics since Sraffa? / Qu’a-t-on appris sur l’économie classique depuis Sraffa?, pp. 73-96.
-
Poulon, Fréderic. 2015. Economie générale, 8ème édition, Paris : Dunod.
-
Salanti, Andrea. 1985. “Le assunzioni della teoria economica: Un’ipotesi interpretativa”. Note Economiche, 1985(1–2), 64–88.
-
Schmitt, Bernard. 1966. Monnaie, salaires et profits, Paris : Presses Universitaires de France.
-
Schmitt, Bernard. 1984. Inflation, chômage et malformations du capital, Paris & Albeuve : Economica & Castella.
-
Seccareccia, Mario. 1982. “Keynes, Sraffa et l’économie classique : le problème de la mesure de la valeur”, L’Actualité économique, vol. 58, n° 1-2, 1982, p. 115-151., availble at: Seccareccia.
-
Seccareccia, Mario. 2004. “Aspects of a New Conceptual Integration of Keynes’s Treatise on Money and the General Theory: Logical Time Units and Macroeconomic Price Formation”, In: Money Credit and the Role of the State, Essays in honour of Augusto Graziani, Neri Salvadori & Richard Arena ed., Aldershot: Ashgate.
-
Schumpeter, Joseph A. [1911] 1949. The theory of economic development an inquiry into profits, capital, credit, interest, the business cycle, Cambridge, Massachusetts: Harvard University Press.
-
Toporowski, Jan. 1999. The End of Finance: The theory of capital market inflation, financial derivatives and pension fund capitalism, London & New York: Routledge, (Routledge Frontiers of Political Economy, 25).
-
Vallageas, Bernard 2010. “The circuit analysis, the monetary economy of production and the multisectorial analysis. Proposals for a S.N.A. built on income-value. A “detransformation” of prices in values.’. MPRA paper. https://mpra.ub.uni-muenchen.de/58916/1/MPRA_paper_58916.pdf.
-
Vallageas, Bernard 2018. Monnaie, profit et valeur : un essai sur le circuit, l’économie monétaire de production et sur les liens entre la macroéconomie et l’analyse financière des entreprises. http://a.world.prod.model.free.fr/monnaie_profit_valeur.pdf.



